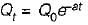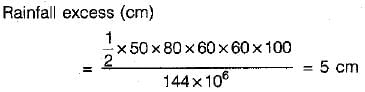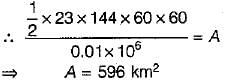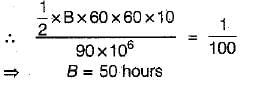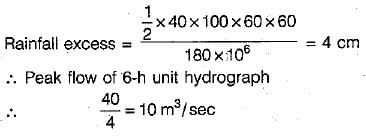Test: Hydrographs - 2 - Civil Engineering (CE) MCQ
10 Questions MCQ Test GATE Civil Engineering (CE) 2025 Mock Test Series - Test: Hydrographs - 2
The recession limb of a flood hydrograph can be expressed with positive values of coefficients, as Qt/Q0 =
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The D-hour unit hydrograph of a catchment may be obtained by dividing the ordinates of a single peak Direct Runoff Hydrograph (DRH) due to a storm of D-hour duration by the
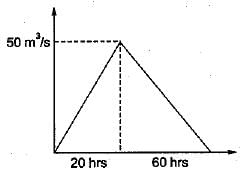
A triangular DRH due to a storm has a time base of 80 hrs and a peak flow of 50 m3/s occurring at 20 hours from the start, if the catchment area is 144 km2, the rainfall excess in the storm was
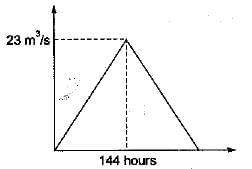
A 12-hr unit hydrograph of a catchment is triangular in shape with a base width of 144 hours and a peak discharge value of 23 m3/s. This unit hydrograph refers to a catchment of area
A 90 km2 catchment has a 4-h unit hydrograph which can be approximated as a triangle. If the peak ordinate of this unit hydrograph is 10m3/s the time base is
A triangular DRH due to a 6-h storm in a catchment has a time base of 100 h and a peak flow of 40 m3/s. The catchment area is 180 km2. The 6-h unit hydrograph of this catchment will have a peak flow in m3/s of
|
31 docs|280 tests
|
|
31 docs|280 tests
|