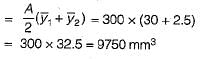Test: Plastic Analysis - 1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test GATE Civil Engineering (CE) 2025 Mock Test Series - Test: Plastic Analysis - 1
The shape factor for a solid circular section of diameter D is equal to
For steel structures proportioned using plastic design, the working load (dead load + imposed load) should be multiplied by which one of the following minimum load factor?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a plastic analysis of structures, the segment between any two successive plastic hinges is assumed to deform as
Which one of the following is the correct maximum shear capacity of a prismatic beam under plastic design of steel structures?
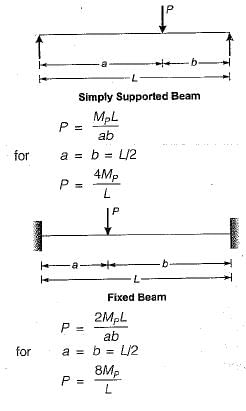
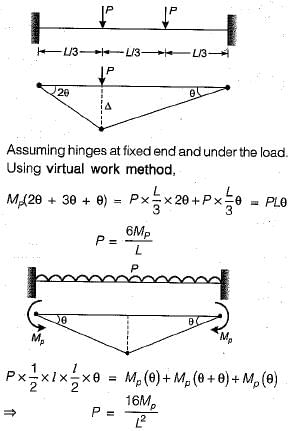
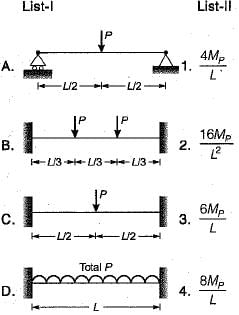
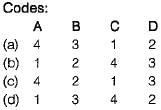
Match List-I (Loaded prismatic beam of uniform Mp) with List-II (Plastic Load) and select the correct answer using the code given below the lists:
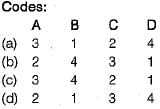
Match List-I (Shape of structural) with List-II (Shape factor) and select the correct answer using the codes given below the lists:

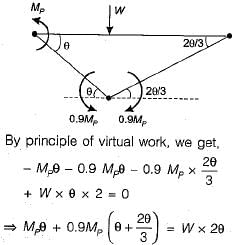
If a uniform beam shown in the figure below has the plastic moment capacity Mp for span AB and 0.9 Mp for span BC, what is the correct virtual work equation?

What is the number of plastic hinges formed if an indeterminate beam with redundancy R is to become determinate?
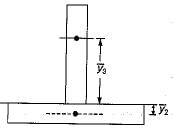
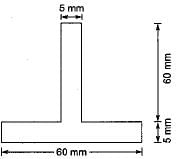
The cross-sectional area and plastic section modulus of the given section are respectively
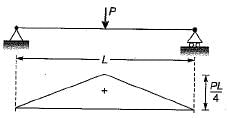
A load P is applied at the middle of a simply supported beam of span L. If the beam is made of ductile material, and Mp is the plastic moment, what is the ultimate value of P?
|
31 docs|280 tests
|
|
31 docs|280 tests
|