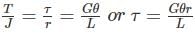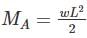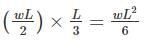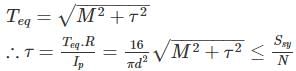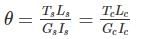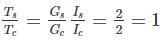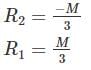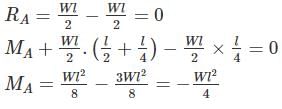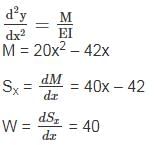Test: Solid Mechanics- 2 - Civil Engineering (CE) MCQ
10 Questions MCQ Test GATE Civil Engineering (CE) 2026 Mock Test Series - Test: Solid Mechanics- 2
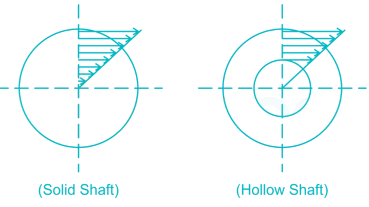
The shear stress at the centre of a circular shaft under torsion is
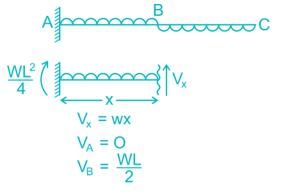
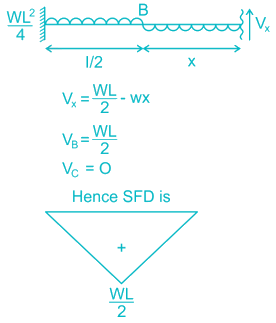
Match List-I with List-II and select the correct answer using the code given below the lists.
List-I (Loaded Beam)
A.
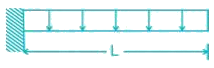
B.
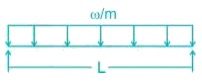
C.
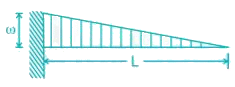
List-II (Maximum Bending moment)
1. 
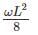
2. 
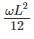
3. 
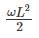
4. 
B.
C.
1.
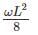
2.
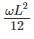
3.
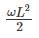
4.
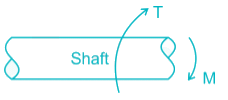
A solid circular shaft of diameter d is subjected to a combined effect of bending moment M and torque T. The relation is used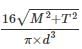 
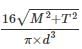for designing the shaft using which one of this material property
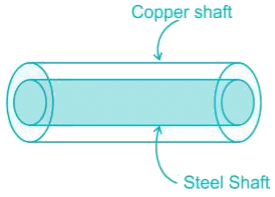
for designing the shaft using which one of this material property
A solid steel shaft is surrounded by a copper shaft, such that, Isteel = 1/2 Icopper. If Gcopper = 1/2 Gsteel, what is the ratio of Ts/Tc if the composite shaft is subjected to a twisting moment?
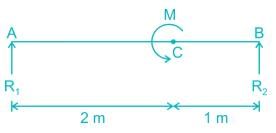
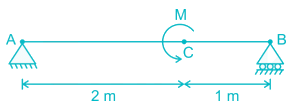
Couple M is applied at C on a simply supported beam AB. The maximum shear force on AC will be
A hollow steel shaft of external diameter 100 mm and internal diameter 50 mm is to be replaced by a solid allow shaft. Assuming the same value of polar modulus for both, the diameter of the solid allows shaft will be-
For a loaded cantilever beam of uniform cross-section, the bending moment (in N-mm) along the length is M(x) = 5x2 + 10x, where x is the distance (in mm) measured from the free end of the beam. The magnitude of shear force (in N) in the cross-section at x = 10 mm is ________.
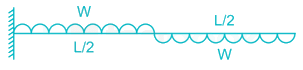
The equation for the deflected shape of a beam carrying a U.D.L and simply supported at ends is given below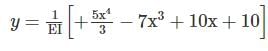 
The load carrying capacity of the beam is
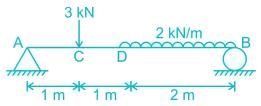
For the given figure, calculate the bending moment (in kN-m) at 2 m from the left end?
|
33 docs|280 tests
|
