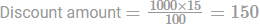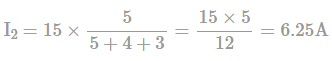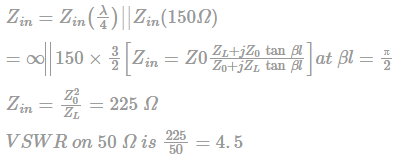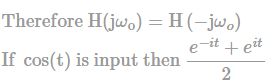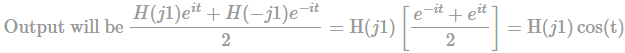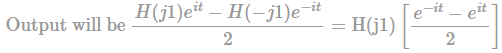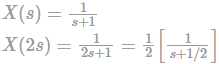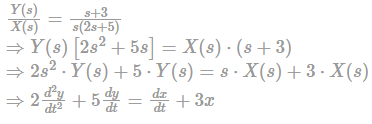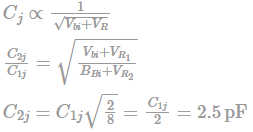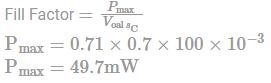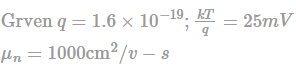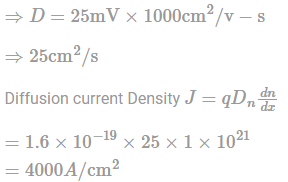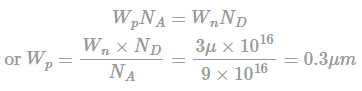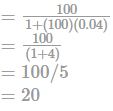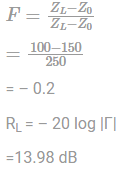Practice Test: Electronics Engineering (ECE)- 13
65 Questions MCQ Test GATE ECE (Electronics) 2023 Mock Test Series | Practice Test: Electronics Engineering (ECE)- 13
| 1 Crore+ students have signed up on EduRev. Have you? |
The average of 8 numbers is 27. If each of the numbers is multiplied by 8, find the average of new set of numbers.
if each no is multiplied by 8 then
The product of two numbers is 2028 and their H.C.F is 13. The numbers of such pair is:
Then, 13a × 13b = 2028
ab = 2028/169 = 12
Now, the co-primes with product 12 are (1, 12) and (3, 4).
So, the required numbers are (13 × 1, 13 × 12) and (13 × 3, 13 × 4).
Clearly, there are 2 such pairs.
Hence, option B is correct.
Which pair of numbers will come in place of the missing numbers.
4,10,__,___, 244,730,2188
Using the same logic, we try to work out the 2 missing numbers as 10 x 3- 2=28
and 28 x 3-2=82. To verify the correctness, we check 244=82 x 3-2
Refer the below data table and answer the following Question.
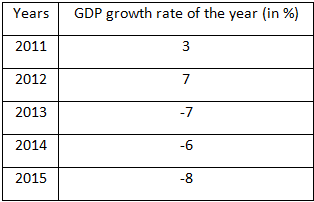
If the GDP of the country was $8 trillion at the end of 2011, what was it at the beginning of 2013?
GDP growth of 2012 = 7%
Therefore at the beginning of 2013, GDP growth = 107% of 8 trillion
= $8.56 trillion
Select the most appropriate synonym of the given word.
Solicit
Sanction means official permission or approval for action.
Scum means a layer of dirt or froth on the surface of a liquid.
Disguise means to give someone or oneself a different appearance in order to conceal one's identity.
In the following question, a sentence is given with a blank to be filled in with an appropriate word. Select the correct alternative out of the four and indicate it by selecting the appropriate option.
The little boy ran ____ fast that he was ____ for breath.
Option B has the correct fillers. Running too fast is less likely to result in a fight for breath but rather a gasp for breath. Hence, ‘so, gasping’ is the most suitable response.
Select the most appropriate option to fill in the blank.
Although his brother is blind, he is very fast _________ calculations.
Let us understand the meaning of the given words :-
"In" = used for expressing the situation of something that is or appears to be enclosed or surrounded by something else.
"With" = accompanied by another person or thing.
"About" = concerning.
"At" = used to show the activity in which someone's ability is being judged.
Since doing fast calculations is an ability, so the preposition "at" is used here.
Hence, option C is the correct answer.
The monthly salaries of A. Band C are in the ratio 2 :3 :5. If C's monthly salary is Rs. 12,000 more than that of A, then B's annual salary is
Let the salaries of A, B and C be 2x, 3x and 5x respectively.
According to the question,
5x - 2x = 12000
⇒ x = 4000
So, monthly Salary of B = 3×4000 = 12000
Therefore Annual Salary = 1212000 = 144000
Mathew told his friend Sham, pointing to a photograph, “Her father is the only son of my mother.” The photograph is of whom?
From the given question, Her father is the only son of my mother indicates that the photograph is of Mathew’s daughter.
Round-trip tickets to a tourist destination are eligible for a discount of 10% on the total fare. In addition, groups of 4 or more get a discount of 5% on the total fare. If the one-way ticket fare of the trip for single person is Rs 100, a group of 5 tourists purchasing round-trip tickets will be charged Rs____.
Total round trip fare for group of 5 tourist without discount = 5x200 = 1000
Discount for Round Trip = 10 % of total fare = (10/100)x1000 = 100 Rs.
Discount for having a group of 5 Tourist = 5 % of total fare
= (5/100) x 1000 = 50 Rs.
Total Discount = Discount for Round + Discount for having a group of 5 Tourist
= 100+50
= 150 Rs.
Thus the net round trip fare for group of 5 tourist after discount is
Net Fare = Total Fare - Total Discount
= 1000-150
= 850 Rs.
One way single person fare = 100
Two way fare for single person = 200
For 5 persons two way fare = 1000
Now, total discount = (10 + 5)% = 15%
Amount to be paid = (1000 - 150) = 850
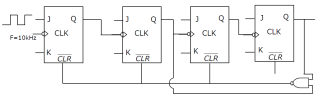
In the following figure, the J and K inputs of all the four Flip-Flops are made high. The frequency of the signal at output Y is
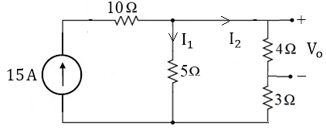
Determine Vo (in Volts) in the given network.
Hence,
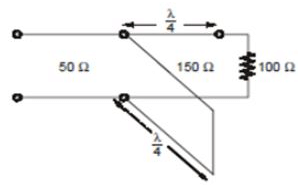
Consider the lossless transmission line circuit shown in the figure, The voltage standing wave ratio on 50 Ω line is given by
The output of a continuous-time, linear time-invariant system is represented by T{x(t)} where x(t) is the input signal. A signal z(t) is called eigen-signal of the system T, when T{z(t)} = Y z(t) , where Y is a complex number, in general, and is called an eigen-value of T. Assume the impulse response of the system T is real and even. Then which of the following statements is TRUE?
Thus H(jω0) will also be real and even
So sin(t) and cos(t) are Eigen signal with same Eigen values.
Given x(t) = e−tu(t). Find the inverse laplace transform of e−3sX(2s).
Taking laplace transform
Taking inverse laplace transform
For the given signal, x(t) = 3 cos 80πt, determine the sampling frequency(in Hz) at which aliasing will take place.
Hence, minimum sampling frequency to avoid aliasing, fs = 2 × 40 = 80Hz
Hence, aliasing will occur if the sampling frequency is less than 80Hz, i.e., at 40Hz.
Find the differential equation of the system described by the transfer function given as:
Let the state transition matrix of a system be given as
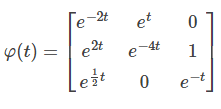
Then which of the following is equal to φ-1(t)
Hence, replace 't' in state transition matrix by '-t'.Thus, option A is the correct answer.
The built-in potential of an abrupt p-n junction is 0.75 V. If its junction capacitance (Q) at a reverse bias (VR) of 1.25 V is 5 pF, the value of CJ (in pF) when VR = 7.25 V is________.
So, answer is 2.5.
A Si Solar cell has short-circuited current of 100 mA and open-circuit voltage of 0.7 V under full illumination. If the fill factor is 0.71 then the Maximum power delivered (in mW) to load by this cell is
Assume electronic charge q = 1.6×10−19C, kT/q = 25mV and electron mobility μn = 1000cm2/V−s. If the concentration gradient of electrons injected into a P-type silicon sample is 1×1021 cm4, the magnitude of electron diffusion current density (in A/cm2) is _________.
From Einstein relation,
In an abrupt p-n junction, the doping concentrations on the p-side and n-side are NA = 9 X 1016 /cm3 and ND = 1 X 1016 /cm3 respectively. The p-n junction is reverse biased and the n-side depletion width is 3μm. The depletion width on the p-side is
The voltage gain of an amplifier is 100. A negative feedback is applied with β = 0.04. The overall gain of the amplifier is:
Then a negative feedback is applied to the amplifier where the gain of the feedback loop is given as β = 0.04
Now the overall gain of the negative feedback amplifier is given as, = A/(1+Aβ)
For common emitter input characteristics VCE is 6V and VBE is changed from 0.32 to 0.8V also base current changes from 40μA to 60μA, then by using the given data calculate the input impedance (in KΩ) kept VCE constant.
hei = ΔVBE/ΔIB|VCE = 6V,
Constant = 0.48V /20μA = 24KΩ
Consider two resistors of 50 kΩ and 100 kΩ at room temperature of 27ºC. These resistors are passing a signal of bandwidth 50 kHz. Let N1 and N2 be the noise voltage generated while operating in series and parallel configuration, respectively. Determine N1 and N2.
T = 300 K
RS = 150 kΩ
RP = 100/3 kΩ.
B = 50 kHz.
We can find out the noise voltage generated through resistors using following formula,
where k is Boltzmann constant.
Thus, N1(Series) would be 11.15 µV and N2(Parallel) would be 5.25 µV.
A receiver has been operating at 290 K and receiving a signal of bandwidth 400 kHz. The amplifier used in the receiver has an average output resistance of 1.5 kΩ. This will lead to Johnson noise voltage of ________ μV.
We have, k = 1.38 × 10-23 J/K,
T = 290 K, B = 400 × 103 Hz,
R = 1.5 × 103Ω
Thus, vn = 3.099 μV.
An amplifier operating over the frequency range of 18 to 20 MHz has a 10kΩ input resistance. The RMS noise voltage at the input to the amplifier at ambient temperature is (assume Boltzman’s constant 
The return loss due to a 150W cable terminated by a 100W load is _______________ (in dB)
What is the maximum torque (in Nm) on a square loop of 200 turns in a field of uniform flux density of 1 Wb/m2. The loop has 15cm side and carries a current of 5A.
N-no of turns = 200
B = 1 Wb/m2
I = 5A
S-area of loop=(15 x 10-2)2 = 0.0225
Tmax = 200×1×5×0.0225 = 22.5Nm
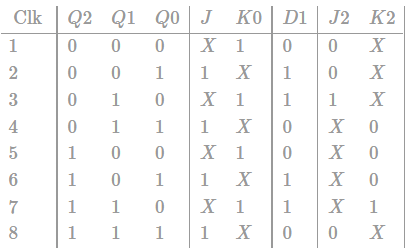
Consider the following sequential circuit consisting of 2 J-K flip flops and D flip flop :
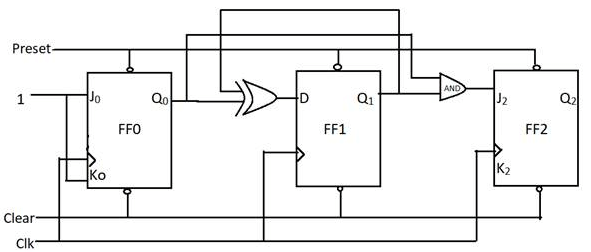
The Mod value for this counter is_____________.
Hence Mod value of the counter is 8.
The maximum number of Boolean expression that can be formed for the function f(x,y,z) satisfying the relation
Effectively there are only four rows for the truth table of the function f(x,y,z).
∴ Total Boolean expression possible is 24 = 16
When two 8-bit numbers A7…A0 and B7…B0 in 2’s complement representation (with A0 and B0 as the least significant bits) are added using a ripple-carry adder, the sum bits obtained are S7….S0 and the carry bits are C7…..C0. An overflow is said to have occurred if
Overflow flag indicates an overflow condition for a signed operation. Some points to remember in a signed operation:
* MSB is always reserved to indicate sign of the number.
* Negative numbers are represented in 2’s – complement.
* An overflow results in invalid operation.
2's complement overflow rules:
* If the sum of two positive numbers yields a negative result, the sum has- overflowed.
* If the sum of two negative number yields a positive result, the sum has overflowed.
* Otherwise, the sum has not overflowed.
Overflow for signed numbers occurs when the carry-in into the MSB (most significant bit) is not equal to carry-out. Conveniently, an XOR-operation on these two bits can quickly determine if an overflow condition exists.
Therefore,
If 
then z lies on where w and z are complex numbers
Two linearly independent solutions of the homogeneous equation, x2y” + xy’ + y = 0 , are
x2y′′ + xy + y = 0
⇒(θ(θ − 1) + θ + 1)y = 0
⇒ (θ2 − θ + θ + 1)y = 0
⇒ (θ2 + 1)y = 0
AE is m2 + 1 = 0
⇒ m = ±i
⇒ CF = C1cosz + C2sinz
∴ Solution is y = C1cos(In x) + C2 sin(In x)
In a broadcast super heterodyne receiver the quality factor of antenna coupling circuit is 150, if the intermediate frequency is 455 KHz, then the image rejection ratio at 20 MHz is.
What is the expression for the minimum conductivity σmin?
The conductivity is given as
σ = q (n µn + p µp)
Since, the electron concentration for minimum conductivity is
Hence, we get the minimum conductivity as
A 700 mW maximum power dissipation diode at 25 °C has 5 mW/oC de-rating factor. If the forward voltage drop remains constant at 0.7 V, the maximum forward current at 65 °C is
Power derating factor dW/dt = -5m W / °C
So power available at 65°C
A Ge sample at room temperature has intrinsic carrier concentration, n = 1.5 × 1013 cm-3 and is uniformly doped with acceptor of 3 × 1016 cm-3 and donor of 2.5 × 1015 cm-3 . Then, the minority charge carrier concentration is:
As the semiconductor is added with both type of impurities i.e. acceptor and donor type both. It is very clear that acceptor type doping is more than the donor type doping and the net effecting doping will be acceptor. Hence, the resultant semiconductor will behave as p-type.
Majority carrier concentration
Therefore,
Minority carrier concentration
What is the image rejection ratio when a super heterodyne receiver with quality factor of 50 is tuned with fs = 800 KHz and local oscillator frequency is 1250 KHz.
The transistor in the amplifier circuit shown in figure is biased at IC = 1 mA. Use VT = 26 mV , β = 200,rb = 0 and r0 → ∞
What is the required value of CE for the circuit to have a lower cut off frequency of 10Hz is
Cut off frequency due to CE is obtained as
Req → Equivalent Resistance seen through capacitor
Trans conductance
A shooter P hits the target with probability of 1/2 but is allowed only one shot whereas the shooter Q hits with probability of 1/4 but takes two shots. A shooter R hits with probability of 1/8 and is allowed five shots. In a competition, it is probable that:
P = ½ = 0.5
First, R second, Q third.
Let A ϵ M3 (R) be such that det (A-I) = 0, where I denotes the 3 x 3 identity matrix. If the trace of A = 13 and det A = 32, then the sum of squares of the eigen values of A is _________.
λ1⋅λ2⋅λ3 = 32 ...(2)
and det(A − I) = 0
∴(λ1 − 1)(λ2 − 1)(λ3 − 1) = 0 ...(3)
From (i), (ii) and (iii), we get λ1λ2 + λ1λ3 + λ2λ3 = 44 ...(4)
An angle modulated wave is given as follows x(t) = 50 cos[2π × 106t + 0.001 cos 2π(500)t]
Find the bandwidth of the signal and the instantaneous frequency of the signal at t = 2ms respectively.
Angle of the signal is given by, θ(t) = 2π × 106t + 0.001 cos 2π(500)t
Instantaneous frequency is given by ωi(t)=dθ(t)/dt = 2π × 106 − π sin 1000πt
⇒ fi(t) = 106 − 0.5 sin 1000πt
At t = 2ms fi(0.002) = 106 − 0.5 sin 2π = 106 Hz = 1M Hz
Frequency deviation: |Δω| = π
Message signal is of the form, m(t) = Am cos 1000πt
Thus, ωm = 1000π
Bandwidth of message signal is given by B = 500Hz
Deviation ratio is given as, β = Δω/ωm = 0.001
By Carson's rule, the bandwidth of the angle modulated signal is given by, BW = 2(β + 1)B = 1001 Hz
The inverse fourier transform of e-6ωu(ω) + e6ωu(ω)
Consider the state-variable model of the system given by
The transfer function of the system is given by
Taking Laplace transform on both sides of the state equation, (without initial condition)
The system matrix is given as,
Consider the signal s(t) shown in the figure, which is the output of an AWGN (Additive White Gaussian Noise) channel with two-sided noise PSD (Power Spectral Density) of 0.5W/Hz. If the signal is given as an input to a matched filter to s(t), then the slope of the output signal for 2V.
Matched filter impulse, h(t) = s*(2 - t) = s(2 - t) = s(t) [from the figure]
Slope (for \(2We have, Noise PSD (two-sided) = N0/2 = 1/2 W/Hz And bit energy or energy of signal s(t), Eb = 22 x 2 = 8Vs
Maximum output SNR 
SNRs = 10 log10 16 = 12.04dB ≈ 12dB
Constellation diagram of a binary modulation scheme is given below.
The two equiprobable symbols shown in the diagram are transmitted through an AWGN (Additive White Gaussian Noise) channel with one-sided PSD (Power Spectral Density) of 0.5W/Hz. If the correlator receiver with optimum threshold detection is used at the receiver end, then the bit error rate (BER) of the system is given by,
Optimum threshold boundary is shown,
The distance between the signalling points is, d = 2√2
Two-sided PSD of noise = Variance(σ2) = N0/2 = 0.5/2 = 1/4 W/Hz Thus, bit error rate or probability of error is.
Find the resonant frequency (in Hz) of the circuit given below:
[Write the Answer upto two decimal point]
L1 = 6 − 1 − 3 = 2H
For second inductor after the first inductor:
L2 = 6 + 2 − 1 = 7H
For the Last Inductor:
L3 = 6 + 2 − 3 = 5H
Equivalent Inductance, Leq = L1 + L2 + L3 = 14H
Resonance frequency is given by,
If Vc(t) = 4 cos (105t) Volts in the circuit given below, then find the value of Vz
We have,
Applying KVL, we get,
Thus 
The Figure shows two signals x(t) and h(t) as
Which of the waveform in the options corresponds to 
denotes convolution.
Consider the causal discrete time system shown below, minimum magnitude of K for which system become unstable is
Has pole at k/2 and for causal and stable pole should be inside unit circle so
|k| < 2="" (for="" stable="" />
Hence for unstable system |k| ≥ 2
Consider a discrete time periodic signal of period N = 6 of whose one period is given as follows
The discrete time Fourier series coefficients of x[n] is given as
Discrete time Fourier series coefficients are given by Where,
In the given oscillator circuit, find the values of C1 and C2 that would make the bridge balanced
Here, the given oscillator circuit is a Wein Bridge oscillator. The condition for the bridge to be balanced is,
Since, R1 = 10 kΩ, R2 = 1 kΩ, R3 = 2 kΩ and R4 = 100 Ω.
Then, C2/C1 ratio would be 10:1.
C1 = 100 µF and C2 = 1 mF satisfies this ratio.
A speech signal, band limited to 5 KHz with peak to peak between +10 V to – 10 V and the signal is sampled at Nyquist rate and the bits 0 and 1 are transmitted using bipolar pulses. What is minimum bandwidth for distortion free transmission ….
While using polar pulses, the minimum bandwidth required is four times the theoretical bandwidth or nyquist bandwidth.
Required BW = 4 * Nyquist BW
= 4 × 2 fm = 4 × 2 × 5 KHz = 40 KHz
Two identical transistors are cascaded as follows with β = 100. The overall voltage gain would be
First we need to analyse this circuit and find out the DC voltages at first and second stages.
First Stage,
DC Voltage at Base of stage 1 = 10*(R2/(R1 + R2)) = 1.67 V.
VE1 = 1.67 – 0.7 = 0.97 V
IE1 = 0.97 V/4.5 kΩ = 0.22 mA
IC1 = 0.22 mA
VC1 = 10 – 0.22×20 = 5.6 V
Second Stage,
Base Voltage = 5.6 V
VE2 = 5.6 – 0.7 = 4.9 V
IE2 = 4.9 V/10 kΩ = 0.49 mA
VC2 = 10 – 0.49*10 = 5.1 V
Overall Voltage gain is given by,
Total output impedance of stage 1 is R3‖Zin. Where Zin is input impedance of second stage.
Total output impedance is R3‖Zin. 4.85 kΩ
And Input impedance,
Then voltage gain of first stage is
Voltage gain of second stage, since there is no loading effect, Output Impedance
= R5 = 10kΩ
Input impedance was found earlier, re2 = 51.02Ω
Overall Voltage gain is Av = Av1 * Av2 = 8363
A radio antenna pointed in a direction of the sky has a noise temperature of 50 kHz. The antenna feeds the received signal to the preamplifier which has a gain of 35 dB over a bandwidth of 10 MHz and a noise figure of 2 dB. Then the noise power at output of the preamplifier is _____(pW)
And therefore Te = 169.62ºK
To determine the output power we have
Where 10 logG = 35, and therefore,
G = 103.5 = 3162. From this we obtain
A load of 1 KΩ is connected to a diode detector which is shunted by a 10kpF capacitor. The diode has a forward resistance of 1 Ω. The maximum permissible depth of modulation, so as to avoid diagonal clipping and modulating signal frequency of 10kHz will be
We know,
On putting these values in (1) we will get,
An n-type silicon sample is uniformly illuminated with light which generates 1020 electron hole pairs per cm3 second. The minority carrier lifetime in the sample is 1 μs. In the steady state, the hole concentration in the sample is approximately 10x, where x is an integer. The value of x is___
Rate of generation = 1020 electron-hole pairs per cm3 per second.
At steady state (at the end of lifetime) t = 1μsec, concentration of hole-electron pair in 1 μsec is
= 1020 ×10–6 = 1014
So, x = 1
In an air-filled rectangular waveguide with a = 2.286cm and b = 1.016cm , the y-component of the TE mode is given by
Then the intrinsic impedance (in Ω) is
A coaxial capacitor of inner radius 1 mm and outer radius 5 mm has a capacitance per unit length of 172 pF/m. If the ratio of outer radius to inner radius is doubled, the capacitance per unit length (in pF/m) is ___.
The intermediate frequency of an AM superheterodyne receiver is 460kHz and the local oscillator frequency {fLO) of the mixer is set at the higher of the two possible values, such that fLO > fc always. If the carries frequency {fC of the receiver signal is 700kHz, then the carrier frequency of the corresponding image signal will be kHz
Given that fc = 700 kHz
fIF - 460 kHz and fLO > fc
So, the carrier frequency of the corresponding image signal can be given as
Which of the above statements is correct?
As we know,
Therefore, on solving
Pick out the 'TRUE' from the following?
16’s complement of a Hex number = 2's complement of it
Ex: 7BH:- 15c ⇒ subtract each digit/symbol from F
16th complement of 7BH
FF -78 = 84+1 = 85H
78 H in 16th complement = 85 H
2's complement of 7B H
7BH = (01111011)2
2’s Complement 7B H = (10000101) = 85 H
So Option (A) is False because BCD = Binary only for ≤ 9
Option (B) is False because compliment of positive number is its magnitude only.
Option (C) is False because Gray code depends on binary but not on BCD.
A dc voltage of 10 V is applied across an n-type silicon bar having a rectangular cross-section and a length of 1 cm as shown in figure. The donor doping concentration ND and the mobility of electrons μs are 1016 cm-3 and 1000 cm2V–1s–1, respectively. The average time (in μs) taken by the electrons to move from one end of the bar to other end is__________
Correct answer is 100.
Assuming that flip-flops are in reset condition initially, the count sequence observed at QA in the circuit shown is
Initially, QA = QB = QC = 0
DA = QB ⊕ QC = 0, DB = QA = 0
DC = QB = 0
After one clock pulse,
QA = 1, QB = 0, QC = 0
DA = QB⊕QC = 0
DB = QA = 1, DC = QB = 0
After two clock pulse,
QA = 1, QB = 1, QC = 0
DA = QB⊕QC = 1
DB = QA = 1, DC = QB = 1
After three clock pulses,
QA = 0, QB = 1, QC = 1
DA = QB⊕QC = 0
DB = QA = 0, DC = QB = 1
After four clock pulse,
QA = 1, QB = 0, QC = 1
DA = QB⊕QC = 1
DB = QA = 1, DC = QB = 0
After five clock pulse,
QA = 0, QB = 1, QC = 0
DA = QB⊕QC = 1
DB = QA = 0, DC = QB = 1
After six clock pulse,
QA = 0, QB = 0, QC = 1
Therefore, the count sequence observed at QA is 0010111.....
|
21 docs|263 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
21 docs|263 tests
|
Download free EduRev App
Related content with Practice Test: Electronics Engineering (ECE)- 13
|
|
Related tests with Practice Test: Electronics Engineering (ECE)- 13
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
