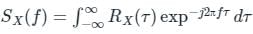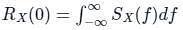Test: Auto Correlation & Power Spectral Density - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Auto Correlation & Power Spectral Density
uto correlation function Rx(τ) of a stationary process X(t) is -
The noise at the input to an ideal frequency detector is white. The power spectral density of the noise at the output is -
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The power spectral density of deterministic signal is given by [sin(f)/f]2. where 'f' is frequency. The auto-correlation function of the signal in the time domain is -
The auto-correction function of white noise is represented as
The power spectral density of white noise is _______ throught the frequency spectrum.
In practice, power spectral density is used to:
Consider a random process X(t) = 3V(t) − 8, where (t) is a zero mean stationary random process with autocorrelation RV(τ) = 4e−5|τ|. The power in X(t) is ________
The autocorrelation of a wide-sense stationary random process is given by: e-2|τ| .The peak value of the spectral density is
If s(f) is the power spectral density of a real, wide sense stationary random process, then which of the following is always true?
|
25 docs|263 tests
|
|
25 docs|263 tests
|


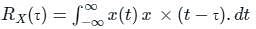
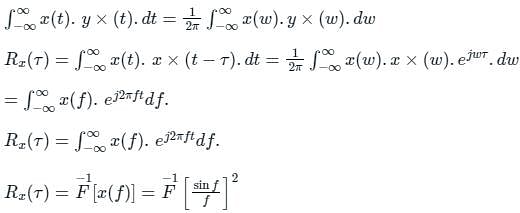
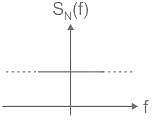
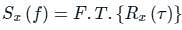
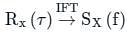
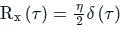
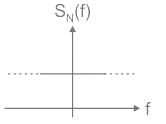
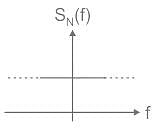
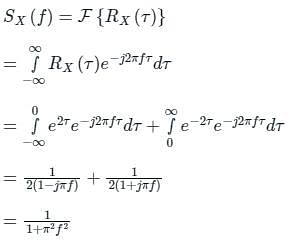 D is at f = 0,
D is at f = 0,