Test: Communication System - Electronics and Communication Engineering (ECE) MCQ
26 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Communication System
The DSB-SC signal recevied at the output of a channel is given as S(t) = 2 cos2π(103 - 0.5). cos2π(106 -
1). Determine the group delay  and phase delay
and phase delay 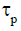 introduced by the channel.
introduced by the channel.
1). Determine the group delay
Which of the following is incorrect about hilbert-transform?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
An amplitude modulated signal is given as s(t) = 14 cos8000πt + 20 cos10000πt + 14 cos12000πt.
Determine the modulation depth.
Determine the modulation depth.
An amplitude modulated signal is given as S(t) = 10 (2 + cos2π x 104t) cos2π x 107t. If the carrier
frequency component is suppresed before transmission, then determine the percentage power
saved.
Suppose that non linear device (NLD) is available for which the output voltage V0 and input voltage Vi are related by V0(t) = a1 where a1 and a3 are constants. Let Vi = m (t) + cos2πfct and a1 = 1, a2 = 1. To generate a DSB-SC signal having carrier frequency is 5MHz, this NLD is followed by a BPF of appropriate centre frequency and band width. Determine fc
Consider a square law device having input voltage Vi and output voltage V0 are related as
This SLD is used to generate an standard AM with a carrier frequency of 3MHz, as shown in the circuit below.
Determine the maximum bandwidth of message signal m(t) so that spectrum of s(t) is nonoverlapping.
A message signal m(t) = 4 cos2πx 104 t is used to generate an FM signal. Determine the minimum
value of (Δf)max so that modulation efficiency is 100%.
A phase-modulated signal is given as S(t) = 30 cos[2πx108t + 100 cos2πx104t]. Determine the
transmission bandwidth required according to carson’s approximation.
Consider an FM signal, S(t) = 10 cos[2π x107t + 10 sin2π x103t]. Determine Kp/Kf if the above modulated signal is assumed phase-modulated signal.
The following message signal m(t) is given to both frequency modulator and phase modulator. If
the maximum phase deviation of both FM and PM is same, determine the Kf/Kp.
Consider a sine wave of frequency 2 KHz and peak amplitude AM. This signal is applied to a delta modulator of step-size 0.4 Volt and sampling period 3.18 x 10-6 sec. What is the maximum power that
may be transmitted without slopeoverload distortion?
A PCM system uses an uniform quantizer followed by a 7-bit binary encoder. The bit rate of the system is equal to 50x106 bits/ second. Determine the output signal to quantization noise ratio when a full-load sinusoidal modulating signal of frequency 1MHz is applied to the input.
An analog signal is sampled, quantized and encoded into a binary PCM system. The specifications of the PCM system include the following: Sampling role = 8 KHz Number of representation levels = 64
Determine the minimum bandwidth required if PCM wave is transmitted over a baseband channel.
A binary PCM system uses pulse P(t) to transmit symbol 1 and - P(t) to transmit symbol 0. The additive noise at the reciever input is white and Gaussian, with zero mean and power spectral density
10-10 W/Hz. Assuming that symbols 1 and 0 occur with equal probability, determine the probability of error at the reciever output.
A source emits one of four symbols S0, S1, S2 and S3 with probabilities 1/3, 1/6, 1/4 and 1/4 respectively.
The successive symbols emitted by the source are statistically independent. Calculate the entropy
of the source.
Consider a sinusoidal signal with random phase, defined by X(t) = where A and fc are constants and θ is a random variable that is uniformly distributed over the interval
Determine the autocorelation function of X (t)
Probability density function of a random variable X is given below

P (X ≤ 4) is
A 1W video signal having bandwidth of 200 MHz is transmitted to a reciver through a cable that has 50 dB loss. If the efficitive two sided noise power spectred density at the receiver is 10-20 Watt/Hz, then the signal to noise ratio at the receiver is
A computer puts out binary data at the rate of 56 kbps. The computer output is transmitted using a
baseband binary PAM system that is designed to have a raised cosine spectrum. Determine band width
required if the roll-off factor is 0.5.
A QPSK system transmits binary data at the rate of 2.5 x 106 bit per second. Determine minimum
bandwidth required for the transmission.
The pulse shown in the figure, is given as the input of a matched filter. Determine the peak value of
the output of matched filter.
A binary random variable X takes the value of 1 with probability 2/3. X is input to a binary symetric
channel with cross-over probability 1/2.
Determine the value of H(Y)
A voice-grade channel of the telephone network has a bandwidth of 3.4 KHz calculate the information capacity of the telephone channel for a signal to noise ratio of 30 dB.
Determine the minimum sampling frequency of x(2t), where x(t) = sine (1000t)
The probability density function of random variable X is given as
Determine the variance (σ2) of random variable X.
|
25 docs|263 tests
|
|
25 docs|263 tests
|


















