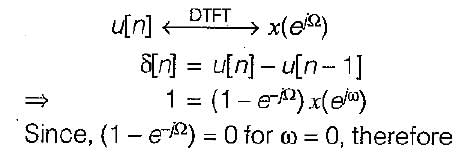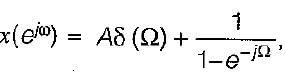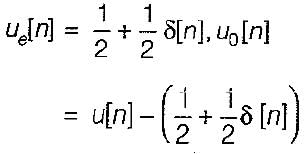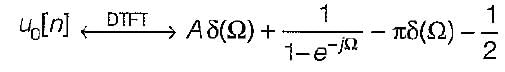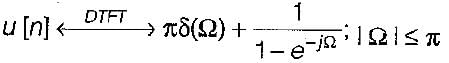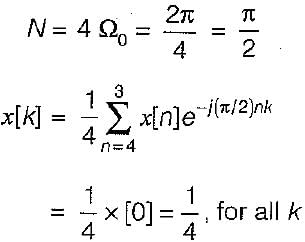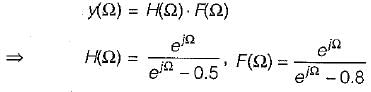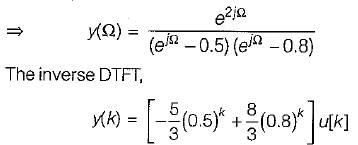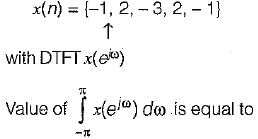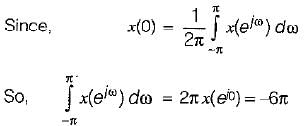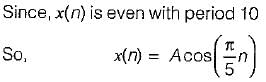Test: Fourier Analysis of Discrete Time Signals - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Fourier Analysis of Discrete Time Signals
The discrete timefourier transform for the given signal x[n] - u[n] is
The discrete time Fourier coefficients x[k] of the signal x [n ] =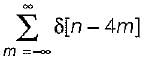
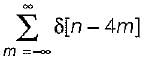
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The zero state respone y(k) for input f(k) = (0.8)k u(k) is
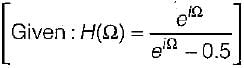
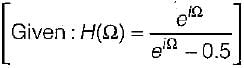
Consider a signal x(n) with following factors:
1. x(n) is real and even signal
2. The period of x(n) is N = 10
3. x(11) = 5
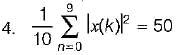
The signal x(n) is
Consider a discrete time signal x(n) = {-1, 2, -3, 2, -1} value of ∠x(eiω) is equal to
A low pass filter with impulse response h1(n) has spectrum H1 (eiω) shown below.
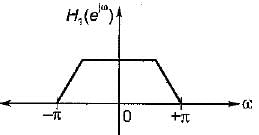
Here only one period has been shown by reversing every second sign of h1(n) a new filter having impulse response h2(t) is created. The spectrum of H2(eiω) is given by
A red signal x[n] with Fourier transform x(eiΩ) has following property:
1. x[n] = 0 for, n > 0
2. x [ 0] > 0
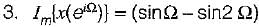
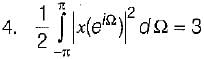
The signal x[n] is
A causal and stable LTI system has the property that,

The frequency response H(eiΩ) for this system is
A 5-point sequence x[n] is given as 4 [- 3] = 1, x[ - 2] = 1, x[ -1 ] = 0 . x[0] = 5 , x[1] - 1
Let x(eiω) denote the discrete time fourier transform of x[n].
The value of 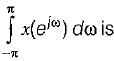
|
25 docs|263 tests
|
|
25 docs|263 tests
|