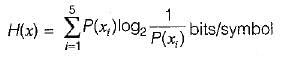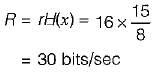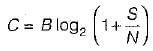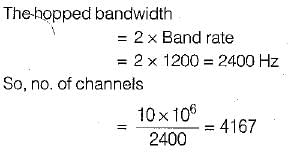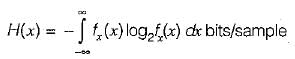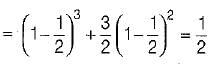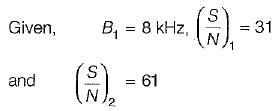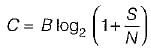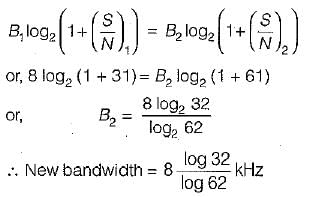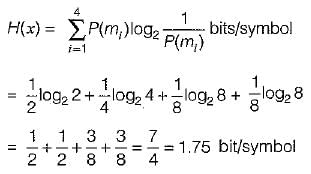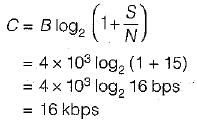Test: Information Theory & Coding
10 Questions MCQ Test GATE ECE (Electronics) 2023 Mock Test Series | Test: Information Theory & Coding
| 1 Crore+ students have signed up on EduRev. Have you? |
The probabilities of the five possible outcomes of an experiment are given as:
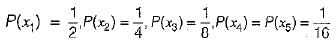
If there are 16 outcomes per second then the rate of information would be equal to
The entropy of the system is
or
Now, rate of outcome r= 16 outcomes/sec (Given)
∴ The rate of information R is
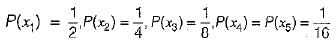
Consider the binary Hamming code of block length 31 and rate equal to (26/31). Its minimum distance is
Minimum distance in hamming code = 3.
Assertion (A): The Shannon-Hartley law shows that we can exchange increased bandwidth for decreased signal power for a system with given capacity C.
Reason (R): The bandwidth and the signal power place a restriction upon the rate of information that can be transmitted by a channel.
Reason (R): The bandwidth and the signal power place a restriction upon the rate of information that can be transmitted by a channel.
According to Shannon-Hartley faw, the channel capacity is expressed as
Thus, if signal power is more, bandwidth will be less and vice-versa. Thus, assertion is a true statement. Reason is also a true statement because the rate of information that can be transmitted depends on bandwidth and signal to noise power. Thus, both assertion and reason are true but reason is not the correct explanation of assertion.
A 1200 band data stream is to be sent over a non-redundant frequency hopping system, The maximum bandwidth for the spread spectrum signal is 10 MHz. if no overlap occurs, the number of channels are equal to
The differential entropy H(x) of the uniformly distributed random variable* with the following probability density function for a = 1 is
We know that the differential entropy of x is given by
Using the given probability density function, we have:
for
a = 1, H(x) = log2 1 = 0
During transmission over a communication channel bit errors occurs independently with probability 1/2 . If a block of 3 bits are transmitted the probability of at least one bit error is equal to
(1 - p)n + np{ 1 - p)n-1 = Required probability
(Here, n = no. of bits and p = probability) ∴ Required probability
A channel has a bandwidth of 8 kHz and signal to noise ratio of 31. For same channel capacity, if the signal to noise ratio is increased to 61, then, the new channel bandwidth would be equal to
We know that channel capacity is
Since channel capacity remains constant, therefore
A source generates 4 messages. The entropy of the source will be maximum when
A source delivers symbols m1, m2, m3 and m4 with probabilities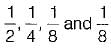 
respectively.
The entropy of the system is
The entropy of the system is
A communication channel with AWGN has a BW of 4 kHz and an SNR pf 15. Its channel capacity is
Channel capacity is
|
21 docs|263 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
21 docs|263 tests
|
Download free EduRev App
Related content with Test: Information Theory & Coding
|
|
|
|
Related tests with Test: Information Theory & Coding
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
