Test: Random Variables - Electronics and Communication Engineering (ECE) MCQ
20 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Random Variables
The number of cars arriving at ICICI bank drive-in window during 10-min period is Poisson random variable X with b = 2.
Que : The probability that more than 3 cars will arrive during any 10 min period is
The number of cars arriving at ICICI bank drive-in window during 10-min period is Poisson random variable X with b = 2.
Que: The probability that no car will arrive is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The power reflected from an aircraft of complicated shape that is received by a radar can be described by an exponential random variable W. The density of W is
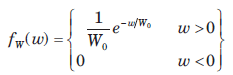
where W0 is the average amount of received power. The probability that the received power is larger than the power received on the average is
Delhi averages three murder per week and their occurrences follow a poission distribution
Que: The probability that there will be five or more murder in a given week is
Delhi averages three murder per week and their occurrences follow a poission distribution
Que: On the average, how many weeks a year can Delhi expect to have no murders ?
Delhi averages three murder per week and their occurrences follow a poission distribution.
Que:How many weeds per year (average) can the Delhi expect the number of murders per week to equal orexceed the average number per week ?
A discrete random variable X has possible values x i = i2 i =1, 2, 3, 4 which occur with probabilities 0.4, 0.25, 0.15, 0.1,. The mean value
The random variable X is defined by the density
The expected value of g(X) = X3 is
The random variables X and Y have variances 0.2 and 0.5 respectively. Let Z= 5X-2Y. The variance of Z is?
The variance of the random variable X with probability density function 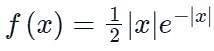 is
is
A Random variable X is uniformly distributed on the interval (-5, 15). Another random variableY = e -X/5 is formed. The value of E[Y ] is
A joint sample space for two random variable X and Y has four elements (1, 1), (2, 2), (3, 3) and (4, 4). Probabilities of these elements are 0.1, 0.35, 0.05 and 0.5 respectively.
Que: The probability of the event {X ≤ 2.5, Y ≤ 6} is
A joint sample space for two random variable X and Y has four elements (1, 1), (2, 2), (3, 3) and (4, 4). Probabilities of these elements are 0.1, 0.35, 0.05 and 0.5 respectively.
Que: The probability of the event {X ≤ 3} is
The statistically independent random variable X and Y have mean values .and
They have second moments
and
Consider a random variable W = 3X - Y.
Que: The mean value E [W] is
The statistically independent random variable X and Y have mean values .and
They have second moments
and
Consider a random variable W = 3X - Y.
Que: The second moment of W is
The statistically independent random variable X and Y have mean values .and
They have second moments
and
Consider a random variable W = 3X - Y.
Que: The variance of the random variable is
Two random variable X and Y have the density function
The X and Y are
The mean value of the random variable
W = (X + 3Y)2 + 2X + 3 is
If machine is not properly adjusted, the product resistance change to the case where ax = 1050Ω . Now the rejected fraction is
|
25 docs|263 tests
|
|
25 docs|263 tests
|


















