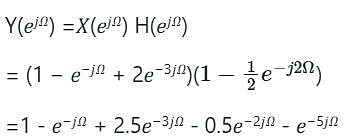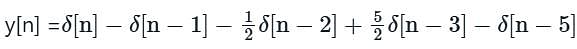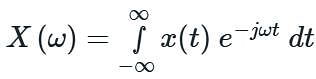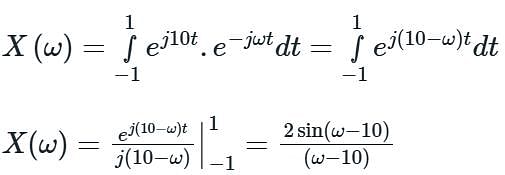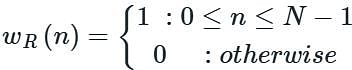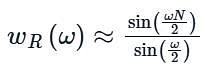Test: The Discrete -Time Fourier Series - Electronics and Communication Engineering (ECE) MCQ
15 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: The Discrete -Time Fourier Series
Consider a periodic signal x[n] with period N and FS coefficients X [k]. Determine the FS coefficients Y [k] of the signal y[n] given in question.
Que: y[n] = x[ n - no]
Consider a periodic signal x[n] with period N and FS coefficients X [k]. Determine the FS coefficients Y [k] of the signal y[n] given in question.
y[n] = x[n] - x[n-2 ]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider a periodic signal x[n] with period N and FS coefficients X [k]. Determine the FS coefficients Y [k] of the signal y[n] given in question.
Que: y[n] = x[n] + x[n + N/2 ] , (assume that N is even)
Consider a periodic signal x[n] with period N and FS coefficients X [k]. Determine the FS coefficients Y [k] of the signal y[n] given in question.
Que: y[n] = x[n] - x[n + N/2 ] , (assume that N is even)
Consider a periodic signal x[n] with period N and FS coefficients X [k]. Determine the FS coefficients Y [k] of the signal y[n] given in question.
Que: y[n] = x*[-n]
Consider a periodic signal x[n] with period N and FS coefficients X [k]. Determine the FS coefficients Y [k] of the signal y[n] given in question.
y[n] = (-1)nx[n], (assume that N is even)
Consider a discrete-time periodic signal
with period N = 10, Also y[n] = x[n] - x[n-1]
Que: The FS coefficients of y[n] are
Consider a discrete-time signal with Fourier representation.
In question the FS coefficient Y [k] is given. Determine the corresponding signal y[n] and choose correct option.
Que: Y[k] = X[k-5] + X[k+5]
onsider a discrete-time signal with Fourier representation.
In question the FS coefficient Y [k] is given. Determine the corresponding signal y[n] and choose correct option.
Que:
Consider a discrete-time signal with Fourier representation.
In question the FS coefficient Y [k] is given. Determine the corresponding signal y[n] and choose correct option.
Que: Y[k] = X[k]*X[k]
Consider a discrete-time signal with Fourier representation.
In question the FS coefficient Y [k] is given. Determine the corresponding signal y[n] and choose correct option.
Que: Y[k] = Re{X[k]}
Consider a signal x[n] with following facts
1. x[n] is a real and even signal
2. The period of x[n] is N = 10
3. X [11] = 5
Let an input x[n] having discrete time Fourier transform  be passed through an LTI system. The frequency response of the LTI system is
be passed through an LTI system. The frequency response of the LTI system is 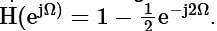 The output y[n] of the system is
The output y[n] of the system is
Consider a signal defined by
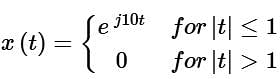
Its Fourier Transform is
The frequency response and the main lobe width for rectangular window are
|
25 docs|263 tests
|
|
25 docs|263 tests
|