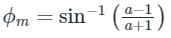Test: Compensators - 1 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Compensators - 1
A system with impulse response is essentially a _______ compensator and used as a ________ filter.
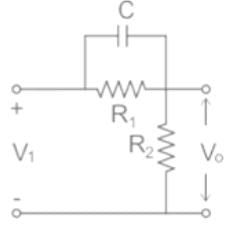
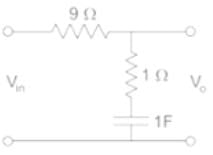
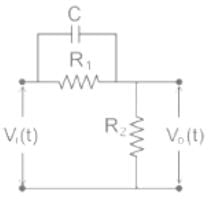
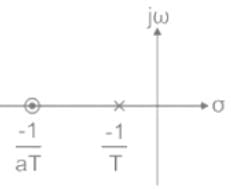
Which of the following is true for the network shown below -

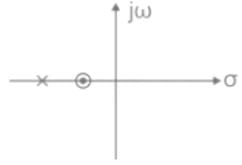
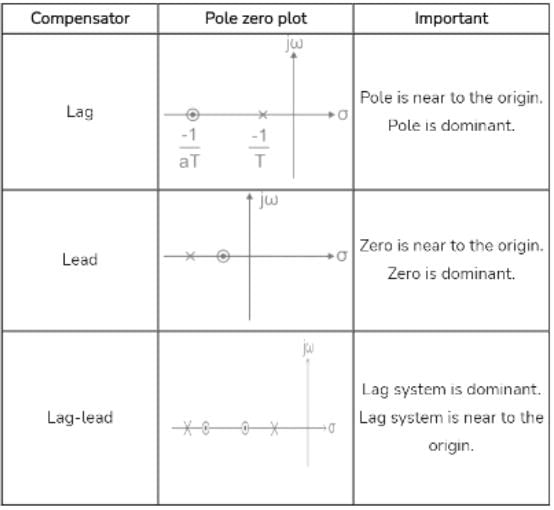
Given a badly underdamped control system, the type of cascade compensator to be used to improve its damping is
The maximum phase shift that can be obtained by using a lead compensator with transfer function Gc(s) =  equal to
equal to
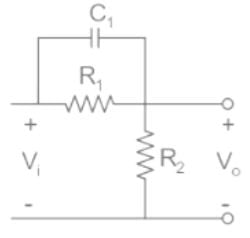
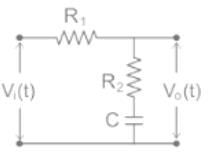
An R-C network has the transfer function
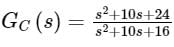
The network could be used as
1. lead compensator
2. lag compensator
3. lag-lead compensator
Which of the above is/are correct?
The compensator required to improve the steady state response of a system is
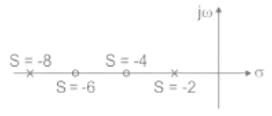
For the network shown in the figure below, the frequency (in rad/s) at which the maximum phase lag occurs is, ___________.
A compensator with the transfer function G(s) = 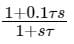 can give maximum gain of
can give maximum gain of
Which of the following is not correct with respect to a phase-lead compensation network?


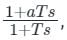 then a < 1
then a < 1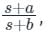 then a > b
then a > b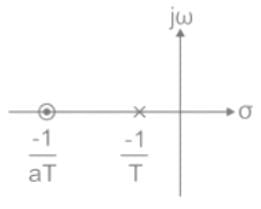
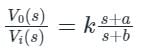
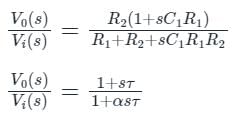
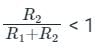

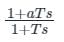

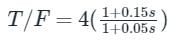
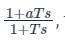 then a < 1
then a < 1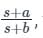 then a > b
then a > b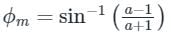
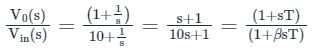
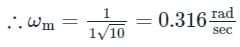
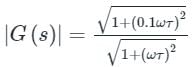
 then a < 1
then a < 1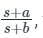 then a > b
then a > b