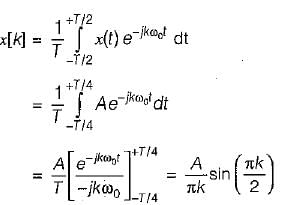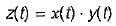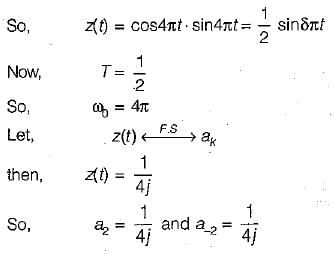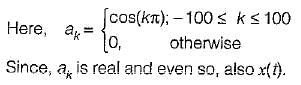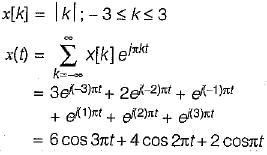Electrical Engineering (EE) > GATE Electrical Engineering (EE) 2024 Mock Test Series > Test: Continuous Time Fourier Series
Test: Continuous Time Fourier Series - Electrical Engineering (EE)
Test Description
8 Questions MCQ Test GATE Electrical Engineering (EE) 2024 Mock Test Series - Test: Continuous Time Fourier Series
Test: Continuous Time Fourier Series for Electrical Engineering (EE) 2023 is part of GATE Electrical Engineering (EE) 2024 Mock Test Series preparation. The Test: Continuous Time Fourier Series questions and answers have been
prepared according to the Electrical Engineering (EE) exam syllabus.The Test: Continuous Time Fourier Series MCQs are made for Electrical Engineering (EE) 2023 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Continuous Time Fourier Series below.
Solutions of Test: Continuous Time Fourier Series questions in English are available as part of our GATE Electrical Engineering (EE) 2024 Mock Test Series for Electrical Engineering (EE) & Test: Continuous Time Fourier Series solutions in
Hindi for GATE Electrical Engineering (EE) 2024 Mock Test Series course. Download more important topics, notes, lectures and mock
test series for Electrical Engineering (EE) Exam by signing up for free. Attempt Test: Continuous Time Fourier Series | 8 questions in 30 minutes | Mock test for Electrical Engineering (EE) preparation | Free important questions MCQ to study GATE Electrical Engineering (EE) 2024 Mock Test Series for Electrical Engineering (EE) Exam | Download free PDF with solutions
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Test: Continuous Time Fourier Series - Question 1
If, f(t) = -f(-t)and f(t) satisfy the dirichlet conditions then f(t) can be expanded in a fourier series containing
Test: Continuous Time Fourier Series - Question 2
The trigonometric Fourier series expansion of an odd function shall have
Test: Continuous Time Fourier Series - Question 3
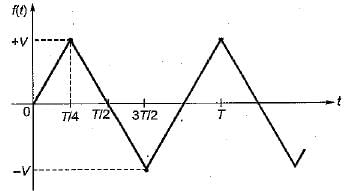
A periodic triangular wave is shown in figure its fourier components will consists only of
Detailed Solution for Test: Continuous Time Fourier Series - Question 3
Test: Continuous Time Fourier Series - Question 4
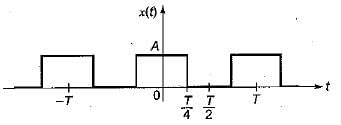
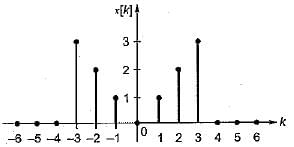
Determine the Fourier series coefficient for given periodic signal x(t) is
Detailed Solution for Test: Continuous Time Fourier Series - Question 4
Test: Continuous Time Fourier Series - Question 5
Consider the three continuous time signals with fundamental period of T = 1/2
x(t) = cos4πt
y(t) = sin 4πt
z(t) = x(t)·y(t)
The Fourier co-efficient of z(t) are given by
Detailed Solution for Test: Continuous Time Fourier Series - Question 5
Test: Continuous Time Fourier Series - Question 6
Consider a continuous time periodic signal x(t) given by
Detailed Solution for Test: Continuous Time Fourier Series - Question 6
Test: Continuous Time Fourier Series - Question 7
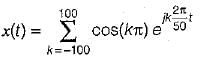
The Fourier series coefficient of time domain signal have been given. Determine the corresponding time domain signal and choose correct option.
Detailed Solution for Test: Continuous Time Fourier Series - Question 7
Test: Continuous Time Fourier Series - Question 8
The Fourier series for f(x) = sin2 x defined over the range -π ≤ x ≤ π is
Detailed Solution for Test: Continuous Time Fourier Series - Question 8
|
23 docs|285 tests
|
Information about Test: Continuous Time Fourier Series Page
In this test you can find the Exam questions for Test: Continuous Time Fourier Series solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Continuous Time Fourier Series, EduRev gives you an ample number of Online tests for practice
|
23 docs|285 tests
|
Download as PDF
Download free EduRev App
Track your progress, build streaks, highlight & save important lessons and more!
Important Questions for Continuous Time Fourier Series
Find all the important questions for Continuous Time Fourier Series at EduRev.Get fully prepared for Continuous Time Fourier Series with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the Continuous Time Fourier Series syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of Continuous Time Fourier Series resources.
Continuous Time Fourier Series MCQs with Answers
Prepare for the Continuous Time Fourier Series within the Electrical Engineering (EE) exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for Continuous Time Fourier Series GATE Electrical Engineering (EE) 2024 Mock Test Series
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace Continuous Time Fourier Series with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup