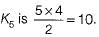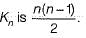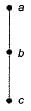Test: Graph Theory- 1 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test GATE Electrical Engineering (EE) Mock Test Series 2025 - Test: Graph Theory- 1
Maximum number of edges in a n-node undirected graph without self loops is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
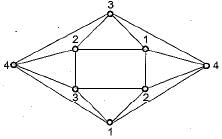
The minimum number of colours required to colour the following graph, such that no two adjacent vertices are assigned the same colour, is

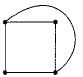
What is the maximum number of edges in an acyclic undirected graph with n vertices?
Let G be the non-planar graph with the minimum possible number of edges. Then G has
Which one of the following is TRUE for any simple connected undirected graph with more than 2 vertices?
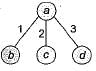
In a binary tree with n nodes, every node has an odd number of descendants. Every node is considered to be its own descendant. What is the number of nodes in the tree that have exactly one child?
The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order. Which of the following sequences can not be the degree sequence of any graph?
I. 7, 6, 5, 4, 4, 3, 2, 1
lI. 6, 6,6, 6, 3, 3, 2, 2
III. 7, 6, 6, 4, 4, 3, 2, 2
IV. 8, 7, 7, 6, 4,2, 1,1
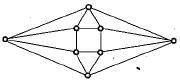
K4 and Q3 are graphs with the following structure:
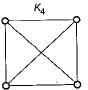
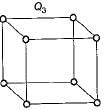
Which one of the following statements is TRUE in relation to these graphs?
|
25 docs|247 tests
|
|
25 docs|247 tests
|