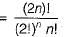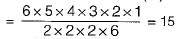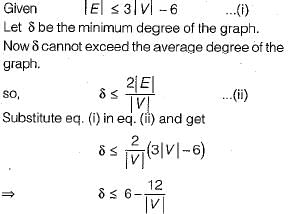Test: Graph Theory- 2 - Electrical Engineering (EE) MCQ
12 Questions MCQ Test GATE Electrical Engineering (EE) Mock Test Series 2025 - Test: Graph Theory- 2
Let G be an arbitrary graph with n nodes and k components. If a vertex is removed from G, the number of components in the resultant graph must necessarily lie between.
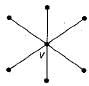
How many perfect matchings are there in a complete graph of 6 vertices?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A Graph G = (V, E) satisfies |E| ≤ 3 |V| - 6. The min-degree of G is defined as 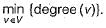
Therefore, min-degree of G cannot be
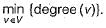
Therefore, min-degree of G cannot be
What is the number of vertices in an undirected connected graph with 27 edges, 6 vertices of degree 2, 3 vertices of degree 4 and remaining of degree 3?
G is a simple, connected, undirected graph. Some vertices of G are of odd degree. Add a node v to G and make it adjacent to each odd degree vertex of G. The resultant graph is sure to be
The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order. Which of the following sequences can not be the degree sequence of any graph?

Which of the following statements is/are TRUE for undirected graph?
P: Number of odd degree vertices is even.
Q: Sum of degrees of all vertices is even.
An ordered n-tuple (d1, d2, .... dn) with d1 ≥ d2 ≥ ... ≥ dn is called graphic if there exists a simple undirected graph with n vertices having degrees d1, d2, ..., dn respectively. Which of the following 6-tuples is NOT graphic?
If G is a forest with n-vertices and k connected components, how many edges does G have?
|
25 docs|247 tests
|
|
25 docs|247 tests
|