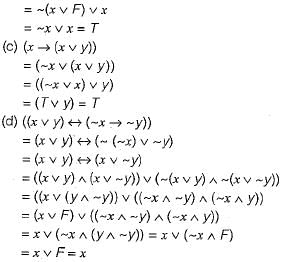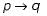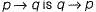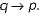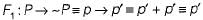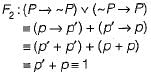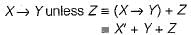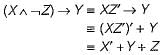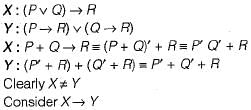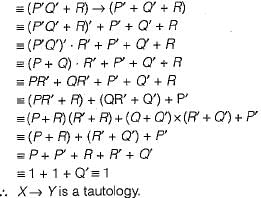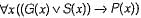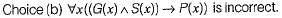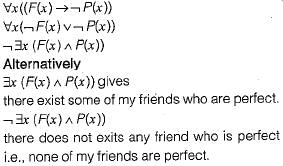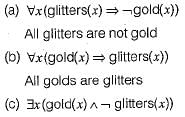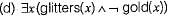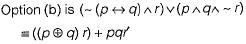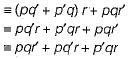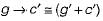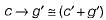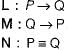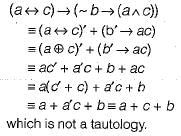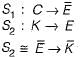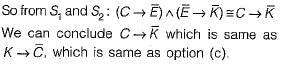Test: Mathematical Logic- 2 - Electrical Engineering (EE) MCQ
13 Questions MCQ Test GATE Electrical Engineering (EE) Mock Test Series 2025 - Test: Mathematical Logic- 2
Which one of the following is false? Read ∧ as AND, v as OR, ~ as NOT, → as one way implication and 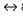 as two way implication.
as two way implication.
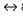 as two way implication.
as two way implication.What is the converse of the following assertion?
I stay only if you go
I stay only if you go
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider two well-formed formulas in propositional logic:
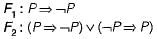
Which of the following statements is correct?
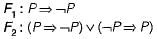
Which of the following statements is correct?
“If X then Y unless Z” is represented by which of the following formulas in propostional logic? ("_") is negation, “∧” is conjunction, and "→" is implication)
Let P, Q and, R be three atomic propositional assertions. Let X denote ( P v Q ) → R and Y denote (P → R) v (Q → R). Which one of the following is a tautology?
Which one of the following is the most appropriate logical formula to represent the statement:
“Gold and silver ornaments are precious”
The following notations are used:
G(x): x is a gold ornament
S(x): x is a silver ornament
P(x): x is precious
Suppose the predicate P(x, y, t) is used to represent the statement that person x can fool person y at time t. Which one of the statements below expresses best the meaning of the formula
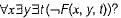
What is the logical translation of the following statements?
“None of my friends are perfect"
Consider the statement:
"Not all that glitters is gold"
Predicate glitters (x) is true if x glitters and predicate gold (x) is true if x is gold. Which one of the following logical formulae represents the above statement?
Which one of the following propositional logic formulas is TRUE when exactly two of p, q, and r are TRUE?
Consider the following statements:
P : Good mobile phones are not cheap
Q : Cheap mobile phones are not good
L : P implies Q
M : Q implies P
N : P is equivalent to Q
Which one of the following about L, M and N is CORRECT?
Which one of the following Boolean expressions is NOT a tautology?
Consider the following two statements:
S1: If a candidate is known to be corrupt, then he will not be elected.
S2: If a candidate is kind, he will be elected.
Which one of the following statements follows from S1 and S2 as per sound inference rules of logic?
|
25 docs|247 tests
|
|
25 docs|247 tests
|