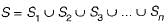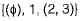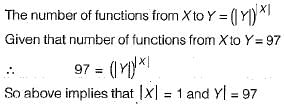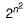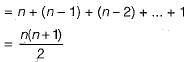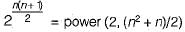Test: Set Theory & Algebra- 1 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test GATE Electrical Engineering (EE) Mock Test Series 2025 - Test: Set Theory & Algebra- 1
Let S be an infinite set and S1, S2, ... Sn be sets such that S1 ∪ S2 ∪ .... ∪ Sn = S. Then
Let A be a finite set of size n. The number of elements in the power set of A x A is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The number of elements in the power set P(S) of the set S = {(φ), 1, (2, 3)} is:
Suppose X and V are sets and |X| and |Y| are their respective cardinalities. It is given that there are exactly 97 functions from X to Y. From this one can conclude that
Suppose A is a finite set with n elements. The number of elements in the Largest equivalence relation of A is
The number of functions from an m element set to an n element set is
The number of binary relations on a set with n elements is
The binary relation S = f (empty set) on set A = {1,2, 3} is
The number of different n x n symmetric matrices with each element being either 0 or 1 is: [Note: power (2, x) is same as 2X]
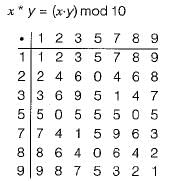
The set {1, 2, 3, 5, 7, 8, 9} under multiplication modulo 10 is not a group. Given below are four possible reasons. Which one of them is false?
|
25 docs|247 tests
|
|
25 docs|247 tests
|