Test: Signals & Systems- 2 - Electrical Engineering (EE) MCQ
20 Questions MCQ Test - Test: Signals & Systems- 2
Consider a continuous rectangular pulse waveform as shown below:
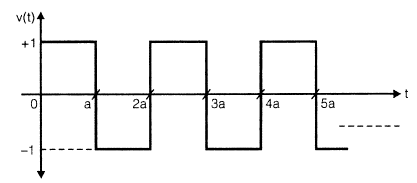
The Laplace tranform of this above waveform is
The Laplace transformation of f(t) is given by F(s).
Given that, 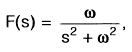 the value of f(t) as t →∞
the value of f(t) as t →∞
The Laplace transform of the signal f(t) = 2e-at sin (bt +θ) is equal to
consider a square pulse f(t) as shown in figure below. Let F(s) denote the Laplace transform of f(t)
then the resulting wave form of the inverse Laplace Transform of F2(s) is
The Laplace Transform of the signal x(t) = (t2 - 2t) u(t - 1)
Consider a LTI system with system function The steady-state response of the system is given by (when the excitation is 8 cos2t)
The Laplace transform of the signal x(t) whose waveform is shown below is given by
A discrete-time system is given by the equation
y(k + 3) = -0.3y(k + 2) + y(k + 1) - 0.5y(k) + 2x(k + 3) - 4x(k + 1)
The highest degree of ‘z’ in Numerator and Denominator polynomials of its transfer function H(z) will be, (Assume all initial conditions are zero).
Consider the discrete time sequence, and
have some ROCs.
- The ROC of X(z) constains the unit circle.
- The ROC of X(z) does not contains the unit circle.
- The discrete sequence x[n], does not have a Fourier transform.
- The discrete sequence x[n] does have a Fourier transform.
Q.
Which is/are correct statement(s)?
If the impulse response of discrete-time sequence is h[n] = an • u[-n - 1], then the system function H(z) equals to, (Assume that α = 1.6)
The z-transform X(z) of a discrete-time sequence x[n] is equals to
It is given that the ROC of X(z) does not includes the unit circle, u[n] = 1 for n ≥ 0. The value of x[n] at n = 1 equals to
Consider a general signal x(t) which is sampled at sampling rate 1/T to get the discrete-time sequence x(kT) having z-transform X(z). Assume X(s) is the Laplace transform of x(t). For X(s) = X(z), which is the correct relation between s and z?
A system is described by the difference equation,
The impulse response of the system is
Consider a waveform f(t)as shown in figure below:
The Fourier series of f(t) have
The Fourier series expansion of a periodic function f(t) contains only odd harmonics of sine waves. It is clearly say that funciton f(t) is an
If X(f) represents the Fourier transform of a signal x(t), which is real and odd symmetric in time, then
A signal x(t) has fourier transform X(ω) which is shown in the figure below:
The value present in the signal x(t) at t =0 is
A source signal s(t) having a Fourier transform as,
The energy and the power that would be observed through a 1 Ω resistor respectively will be
Assuming x(t) is an even function. Then
Fourier transform of x(t) will be:














