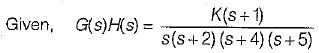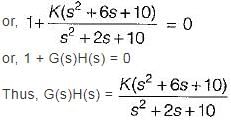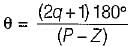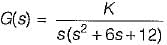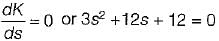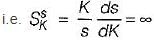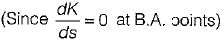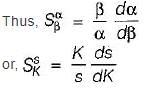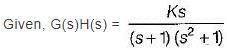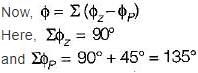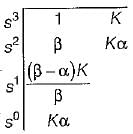Test: The Root Locus Technique- 2
10 Questions MCQ Test GATE Electrical Engineering (EE) 2023 Mock Test Series | Test: The Root Locus Technique- 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The open loop transfer function of a unity feedback control system is given by
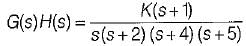
The breakaway point in its root locus will lie between
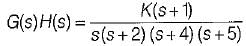
The breakaway point in its root locus will lie between
Here, P = 4,Z = 1, P - Z = 3
No. of branches of RL terminating at zero = 1.
No. of branches of RL terminatina at infinity = 3
Since out of the given option, real axis between s = -2 and s = -4 is only a part of root locus, therefore breakaway point will lie between -2 and -4.
The characteristic equation of a closed loop control system is given by:
s2 + 2s +10 + K(s2 + 6s + 10) = 0
The angle of asymptotes for the root loci for K ≥ 0 are given by
s2 + 2s +10 + K(s2 + 6s + 10) = 0
The angle of asymptotes for the root loci for K ≥ 0 are given by
Given, s2 + 2s + 10 + K(s2 + 6s + 10) = 0
Here, number of open loop poles, P = 2. Number of open loop zero, Z = 2
∴ P - Z = 0.
Angle of asymptotes are given by:
Sines P - Z = 0, therefore there are no angle of asymptotes for the root locus of the given system.
The breakaway point in the root loci plot for the loop transfer function
Given,
1+ G(s) = 0
or, s (s2+ 6 s + 12) + K = 0
or, K = - (s3 + 6s2 + 12s)
For B.A. points,
or, s2 + 4s + 4 = 0
or, (s + 2)2 = 0
or, s = - 2 , - 2
For given O.L.T.F., P = 3, Z = 0, P - Z = 3
Poles are at s = 0 and s = -3 ± j√3 = -3 ± j1.732
Since entire -ve real axis is a part of root locus, therefore s = -2 is a valid breakaway point.
Consider the following statements pertaining to root locus techniques:
1. Routh-Hurwitz criterion may be used to find the intersections of the root loci on the imaginary axis.
2. Breakaway points on the root loci of an equation corresponds to multiple-order roots of the equation.
3. The breakaway points on the root loci of 1 + KG(s) H(s) = 0 must satisfy
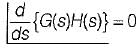
4. n root loci arrive or depart a breakaway point at 180/n degrees.
Which of these statements are correct?
Assertion (A): From the root sensitivity standpoint, a system should not be operated at the breakaway points.
Reason (R): The root sensitivity at the breakaway points is zero.
From the root sensitivity, standpoint, a system should not be operated at the breakaway points because root sensitivity at breakaway point is infinite.
at breakaway points
Here, α = closed loop poles(s)
and β = system gain (K)
Consider the following statements:
1. All the rules and properties for the construction of root loci in the s-plane can be applied to the construction of root loci of discrete data system in the z-plane without any modification.
2. The breakaway points of the root loci must always be on the real axis.
3. There is only, one intersection of the asymptotes of the complex root loci.
4. Adding a pole to Q(s)/P(s) has the general effect of pushing the root loci to the left, whereas adding a zero pushes the loci to the right.
Which of the above statements is/are not correct related to root locus technique in control system?
There is possibility of complex B.A. point. Also when a pole is added to OLTF, root locus pushes to right and reverse happens when a zero is added.
For the loop transfer function:
the angle of departure at s = j for K > 0 is
Here, P = 3, Z = 1, P - Z = 2
No. of branches of RL terminating at zero = 1.
No. of branches of RL termination at infinity = 2
Here, two branches of RL has to terminate at infinity.
Thus, the two imaginary poles will terminate at infinity.
Hence, we need to find angle of departure for which we join all poles and zeros with the imaainarv Dole at s = j1.
Thus, φ = (90° -135°) = - 45°
∴ Angle of departure is,
φD = 180° + φ
= 180° - 45° = 135°
Which of the following is not true regarding the existence of breakaway point in root locus technique?
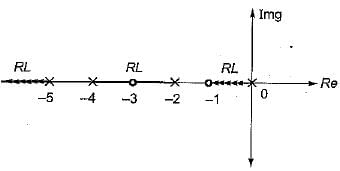
The open loop transfer function of a system is given by
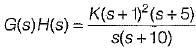
The number of loci terminating at infinity is
Here,
P = 2, Z = 3 and Z > P
∴ No. of branches of RL terminating at infinity
= Z - P = 3 - 2 = 1
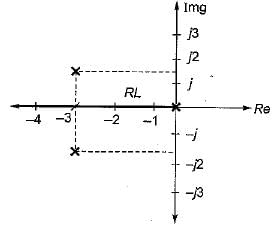
A unity feedback system has open-loop transfer function,
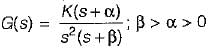
The valid root-loci for this system is
To find whether root locus intersects the imaginary axis or not, we construct Routh’s array. Characteristic equation is
s3 + βs2 + Ks + Kα = 0
Routh's array is:
For β > α > 0, root-loci doesn't intersect the jω-axis and is stable for all positive values of K (no sign change in first column for β > α > 0 and K> 0).
Also, P = 3, Z = 1, P - Z = 2
Thus, two branches of RL will terminate at infinity while one branch will terminate at a zero.
Therefore, possible root locus diagram will be represented by option (a).
|
22 docs|274 tests
|
|
22 docs|274 tests
|
Top Courses for Electronics and Communication Engineering (ECE)
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
