CAT Previous Year Questions: Linear and Quadratic Equations (July 16) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - CAT Previous Year Questions: Linear and Quadratic Equations (July 16)
If x and y are real numbers such that x2 + (x − 2y − 1)2 = −4y(x + y), then the value x−2y is
[2023]
If 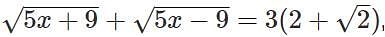 then
then 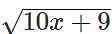 is equal to
is equal to
[2023]
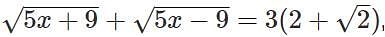 then
then 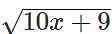 is equal to
is equal to| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The number of integer solutions of equation 2 |x| (x2 + 1)= 5x2 is
[2023]
Let & and β be the two distinct roots of the equation 2x2 - 6x + k = 0, such that (α + β) and αβ are the distinct roots of the equation x2 + px + p = 0. Then, the value of 8(k - p) is
[2023]
The equation x3 + (2r + 1)x2 + (4r - 1)x + 2 = 0 has -2 as one of the roots. If the other two roots are real, then the minimum possible non-negative integer value of r is
[2023]
The sum of all possible values of x satisfying the equation 24x2 - 22x2 + x + 16 + 22x + 30 = 0, is
[2023]
Amal purchases some pens at ₹ 8 each. To sell these, he hires an employee at a fixed wage. He sells 100 of these pens at ₹ 12 each. If the remaining pens are sold at ₹ 11 each, then he makes a net profit of ₹ 300, while he makes a net loss of ₹ 300 if the remaining pens are sold at ₹ 9 each. The wage of the employee, in INR, is
[2021]
A basket of 2 apples, 4 oranges and 6 mangoes costs the same as a basket of 1 apple, 4 oranges and 8 mangoes, or a basket of 8 oranges and 7 mangoes. Then the number of mangoes in a basket of mangoes that has the same cost as the other baskets is
[2021]
Onion is sold for 5 consecutive months at the rate of Rs 10, 20, 25, 25, and 50 per kg, respectively. A family spends a fixed amount of money on onion for each of the first three months, and then spends half that amount on onion for each of the next two months. The average expense for onion, in rupees per kg, for the family over these 5 months is closest to
[2021]
The amount Neeta and Geeta together earn in a day equals what Sita alone earns in 6 days. The amount Sita and Neeta together earn in a day equals what Geeta alone earns in 2 days. The ratio of the daily earnings of the one who earns the most to that of the one who earns the least is
[2021]
|
152 docs|327 tests
|