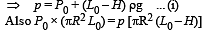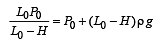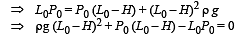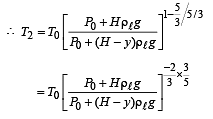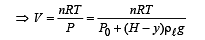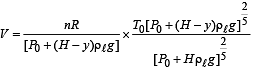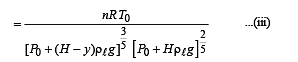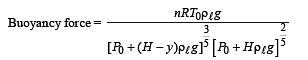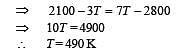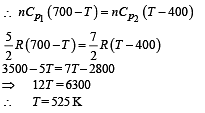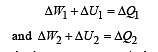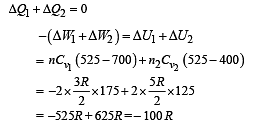JEE Advanced (Single Correct MCQs): Heat & Thermodynamics - JEE MCQ
9 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced (Single Correct MCQs): Heat & Thermodynamics
A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
Q.1. The piston is now pulled out slowly and held at a distance 2L from the top. The pressure in the cylinder between its top and the piston will then be
A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
Q.2. While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
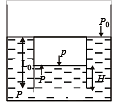
Q.3. The piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brought below the cylinder and put in a position so that the water surface in the tank is at the same level as the top of the cylinder as shown in the figure. The density of the water is r. In equilibrium, the height H of the water column in the cylinder satisfies
A small spherical monoatomic ideal gas bubble (γ = 5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure is P0 (Neglect surface tension).
Q.4. As the bubble moves upwards, besides the buoyancy force the following forces are acting on it
A small spherical monoatomic ideal gas bubble (γ = 5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure is P0 (Neglect surface tension).
Q.5. When the gas bubble is at a height y from the bottom, its temperature is –
A small spherical monoatomic ideal gas bubble (γ = 5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure is P0 (Neglect surface tension).
Q.6. The buoyancy force acting on the gas bubble is (Assume R is the universal gas constant)
In the figure, a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulated material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monatomic gas at 700 K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400 K. The heat capacities per mole of an ideal monatomic gas are 
those for an ideal diatomic gas are 
Q.7. Consider the partition to be rigidly fixed so that it does not move. When equilibrium is achieved, the final temperature of the gases will be
In the figure, a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulated material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monatomic gas at 700 K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400 K. The heat capacities per mole of an ideal monatomic gas are those for an ideal diatomic gas are
Q.8. Now consider the partition to be free to move without friction so that the pressure of gases in both compartments is the same. The total work done by the gases till the time they achieve equilibrium will be
Statement-1 : The total translational kinetic energy of all the molecules of a given mass of an ideal gas is 1.5 times the product of its pressure and its volume. because
Statement-2 : The molecules of a gas collide with each other and the velocities of the molecules change due to the collision.
|
446 docs|930 tests
|
|
446 docs|930 tests
|
Top Courses for JEE
Important Questions for JEE Advanced (Single Correct MCQs): Heat & Thermodynamics
JEE Advanced (Single Correct MCQs): Heat & Thermodynamics
Online Tests for JEE Advanced (Single Correct MCQs): Heat & Thermodynamics Chapter-wise Tests for JEE Main & Advanced
|
© EduRev
|
Education Revolution
|
Follow Us
|
