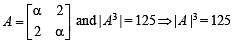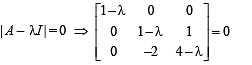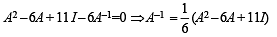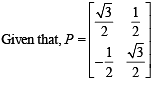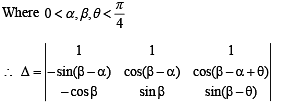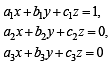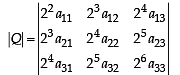JEE Advanced (Single Correct MCQs): Matrices and Determinants - JEE MCQ
21 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced (Single Correct MCQs): Matrices and Determinants
Consider the set A of all determinants of order 3 with entries 0 or 1 only. Let B be the subset of A consisting of all determinants with value 1. Let C be the subset of A consisting of all determinants with value –1. Then
If ω (≠1) is a cube root of unity, then


| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let a, b, c be the real numbers. Then following system of equations in x, y and z
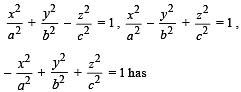
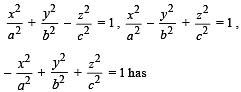
If A and B are square matrices of equal degree, then which one is correct among the followings?
The parameter, on which the value of the determinant  does not depend upon is
does not depend upon is
If the system of equations x – ky – z = 0, kx – y – z = 0, x + y – z = 0 has a non-zero solution, then the possible values of k are
 Then the value of the determinant
Then the value of the determinant 
The number of values of k for which the system of equations (k + 1)x + 8y = 4k; kx + (k + 3) y = 3k – 1 has infinitely many solutions is
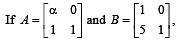 then value of α for which A2 = B, is
then value of α for which A2 = B, is
If the system of equations x + ay = 0, az + y = 0 and ax + z = 0 has infinite solutions, then the value of a is
Given 2x – y + 2z = 2, x – 2y + z = – 4, x + y + λz = 4 then the value of λ such that the given system of equation has NO solution, is
 then the value of α is
then the value of α is

 then the value of c and d are
then the value of c and d are
 and Q = PAPT and x = PTQ2005P then x is equal to
and Q = PAPT and x = PTQ2005P then x is equal to
Consider three points
P = (- sin(β - α), - cosβ), Q = (cos(β-α), sin β) and
R = (cos(β- α+θ), sin(β- θ)) , where 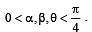
Then,
The number of 3 × 3 matrices A whose entries are either 0 or1 and for which the system  has exactly twodistinct solutions, is
has exactly twodistinct solutions, is
Let ω ≠ 1 be a cube root of unity and S be the set of all non-singular matrices of the form  where each of a, b and c is either ω or ω2. Then the number of distinct matrices in the set S is
where each of a, b and c is either ω or ω2. Then the number of distinct matrices in the set S is
Let P = [aij] be a 3 x 3 matrix and let Q = [bij], where bij = 2i + j aij for 1 < i , j < 3. If the determinant of P is 2, then the determinant of the matrix Q is
If P is a 3 x 3 matrix such that PT = 2P + I, where PT is the transpose of P and I is the 3 x 3 identity matrix, then there
exists a column matrix 
Let 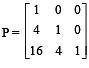 and I be the identity matrix of order 3. If Q = [qij] is a m atrix such that P50 – Q = I, then
and I be the identity matrix of order 3. If Q = [qij] is a m atrix such that P50 – Q = I, then  equals
equals
|
447 docs|930 tests
|
|
447 docs|930 tests
|





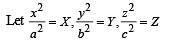

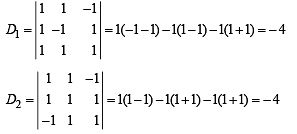

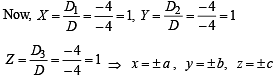

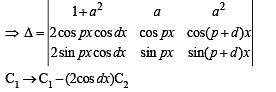

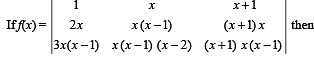

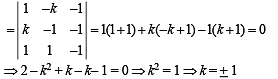

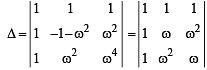
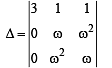 (as 1 + ω + ω2 = 0)
(as 1 + ω + ω2 = 0)