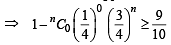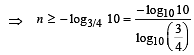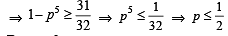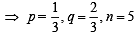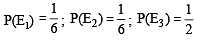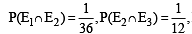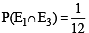Test: 35 Year JEE Previous Year Questions: Probability - JEE MCQ
28 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: 35 Year JEE Previous Year Questions: Probability
A problem in mathematics is given to three students A, B, C and their respective probability of solving the problem
is  and
and  . Probability that the problem is solved is [2002]
. Probability that the problem is solved is [2002]
is
 and
and  . Probability that the problem is solved is [2002]
. Probability that the problem is solved is [2002]A and B are events such that P(A ∪ B)=3/4, P(A ∩ B)=1/4,  is [2002]
is [2002]
 is [2002]
is [2002]| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A dice is tossed 5 times. Getting an odd number is considered a success. Then the variance of distribution of success is [2002]
The mean and variance of a random variable X having binomial distribution are 4 and 2 respectively, then P (X = 1) is
[2003]
Events A, B, C are mutually exclusive events such that and
and  The set of possible values of x are in the interval. [2003]
The set of possible values of x are in the interval. [2003]
Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse is [2003]
The probability that A speaks truth is ,  while the probability for B is .
while the probability for B is . 
The probability that they contradicteach oth er when asked to speak on a fact is [2004]
A random variable X has the probability distribution:  For the events E = {X is a prime number } and F = {X< 4}, the P( E ∪ F) is [2004]
For the events E = {X is a prime number } and F = {X< 4}, the P( E ∪ F) is [2004]
The mean and the variance of a binomial distribution are 4 and 2 respectively. Then the probability of 2 successes is [2004]
Three houses are available in a locality. Three persons apply for the houses. Each applies for one house without consulting others. The probability that all the three apply for the same house is [2005]
A random variable X has Poisson distribution with mean 2.
Then P (X > 1.5) equals [2005]
Let A and B be two events such that 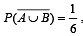
 and
and  where
where  stands forcomplement of event A. Then events A and B are
stands forcomplement of event A. Then events A and B are
At a telephone enquiry system the number of phone cells regarding relevant enquiry follow Poisson distribution with an average of 5 phone calls during 10 minute time intervals.
The probability that there is at the most one phone call during a 10-minute time period is [2006]
Two aeroplanes I and II bomb a target in succession. The probabilities of I and II scoring a hit correctly are 0.3 and 0.2, respectively. The second plane will bomb only if the first misses the target. The probability that the target is hit by the second plane is [2007]
A pair of fair dice is thrown independently three times. The probability of getting a score of exactly 9 twice is [2007]
It is given that the events A and B are such that 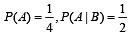 and
and  Then P(B) is [2008]
Then P(B) is [2008]
A die is thrown. Let A be the event that the number obtained is greater than 3. Let B be the event that the number obtained is less than 5. Then P(A∪B) is [2008]
In a binomial distribution  if the probability of at least one success is greater than or equal to
if the probability of at least one success is greater than or equal to  then n is greater than: [2009]
then n is greater than: [2009]
One ticket is selected at random from 50 tickets numbered 00,01,02,...,49. Then the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals: [2009]
Four numbers are chosen at random (without replacement) from the set {1, 2, 3, ...20}. [2010]
Statement -1: The probability that the chosen numbers when arranged in some order will form an AP is 
Statement -2 : If the four chosen numbers form an AP, then the set of all possible values of common difference is (±1, ±2, ±3, ±4,±5) .
An urn contains nine balls of which three are red, four are blue and two are green. Three balls are drawn at random without replacement from the urn. The probability that the three balls have different colours is [2010]
Con sid er 5 in dependen t Ber n oull i’s tr i als each wi th probability of success p. If the probability of at least one failure is greater than or equal to  then p lies in the interval [2011]
then p lies in the interval [2011]
If C and D are two events such that C ⊂ D and P(D) ≠ 0, then the correct statement among the following is [2011]
Three numbers are chosen at random without replacement from {1,2,3,..8}. The probability that their minimum is 3, given that their maximum is 6, is : [2012]
A multiple choice examination has 5 questions. Each question has three alternative answers of which exactly one is correct.
The probability that a student will get 4 or more correct answers just by guessing is: [JEE M 2013]
Let A and B be two events such that 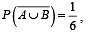

 where
where  stands for the complement of the event A. Then the events A and B are [JEE M 2014]
stands for the complement of the event A. Then the events A and B are [JEE M 2014]
If 12 identical balls are to be placed in 3 identical boxes, then the probability that one of the boxes contains exactly 3 balls is : [JEE M 2015]
Let two fair six-faced dice A and B be thrown simultaneously. If E1 is the event that die A shows up four, E2 is the event that die B shows up two and E3 is the event that the sum of numbers on both dice is odd, then which of the following statements is NOT true ? [JEE M 2016]
|
347 docs|185 tests
|
|
347 docs|185 tests
|







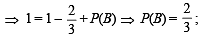




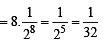
 and
and 
 and
and 










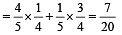
 and n = 8
and n = 8


 =1- P(x = 0) - P(x=1)
=1- P(x = 0) - P(x=1)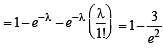
 and
and 
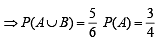
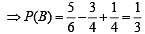
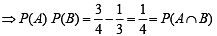

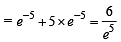
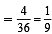
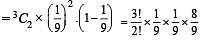
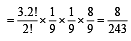
 P(B/A) = 2/3
P(B/A) = 2/3