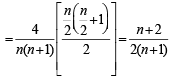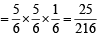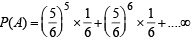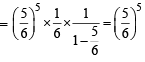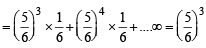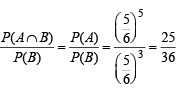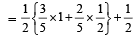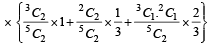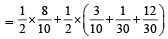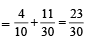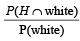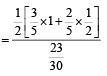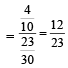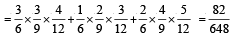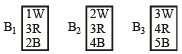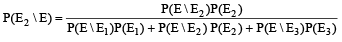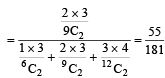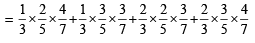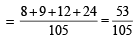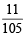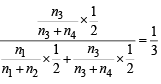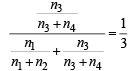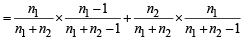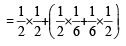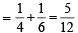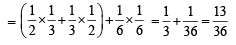Test: Comprehension Based Questions: Probability - JEE MCQ
16 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: Comprehension Based Questions: Probability
PASSAGE - 1
There are n urns, each of these contain n + 1 balls. The ith urn contains i white balls and (n + 1 – i) red balls. Let ui be the event of selecting ith urn, i = 1, 2, 3 .........., n and w the event of getting a white ball.
Q. If P(ui) ∝ i, where i = 1, 2, 3,......., n, then 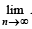 P(w) =(2006 - 5M, –2)
P(w) =(2006 - 5M, –2)
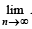 P(w) =(2006 - 5M, –2)
P(w) =(2006 - 5M, –2)PASSAGE - 1
There are n urns, each of these contain n + 1 balls. The ith urn contains i white balls and (n + 1 – i) red balls. Let ui be the event of selecting ith urn, i = 1, 2, 3 .........., n and w the event of getting a white ball.
Q. If P(ui) = c, (a constant) then P(un/w) = (2006 - 5M, –2)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
PASSAGE - 1
There are n urns, each of these contain n + 1 balls. The ith urn contains i white balls and (n + 1 – i) red balls. Let ui be the event of selecting ith urn, i = 1, 2, 3 .........., n and w the event of getting a white ball.
Q. Let P(ui) =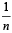 , if n is even and E denotes the event of choosing even numbered urn, then the value of P(w / E) is (2006 - 5M, –2)
, if n is even and E denotes the event of choosing even numbered urn, then the value of P(w / E) is (2006 - 5M, –2)
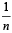 , if n is even and E denotes the event of choosing even numbered urn, then the value of P(w / E) is (2006 - 5M, –2)
, if n is even and E denotes the event of choosing even numbered urn, then the value of P(w / E) is (2006 - 5M, –2)PASSAGE - 2
A fair die is tossed repeatedly until a six is obtained. Let X denote the number of tosses required. (2009)
Q. The probability that X = 3 equals
PASSAGE - 2
A fair die is tossed repeatedly until a six is obtained. Let X denote the number of tosses required. (2009)
Q. 5. The probability that X ≥ 3 equals
PASSAGE - 2
A fair die is tossed repeatedly until a six is obtained. Let X denote the number of tosses required. (2009)
Q.The conditional probability that X ≥ 6 given X > 3 equals
PASSAGE - 3
Let U1 and U2 be two urns such that U1 contains 3 white and 2 red balls, and U2 contains only 1 white ball. A fair coin is tossed. If head appears then 1 ball is drawn at random from U1 and put into U2.
However, if tail appears then 2 balls are drawn at random from U1 and put into U2 . Now 1 ball is drawn at random from U2. (2011)
Q. The probability of the drawn ball from U2 being white is
PASSAGE - 3
Let U1 and U2 be two urns such that U1 contains 3 white and 2 red balls, and U2 contains only 1 white ball. A fair coin is tossed. If head appears then 1 ball is drawn at random from U1 and put into U2.
However, if tail appears then 2 balls are drawn at random from U1 and put into U2 . Now 1 ball is drawn at random from U2. (2011)
Q. Given that the drawn ball from U2 is white, the probability that head appeared on the coin is
PASSAGE - 4
A box B1 contains 1 white ball, 3 red balls and 2 black balls. Another box B2 contains 2 white balls, 3 red balls and 4 black balls. A third box B3 contains 3 white balls, 4 red balls and 5 black balls.
Q. If 1 ball is drawn from each of the boxes B1, B2 and B3, the probability that all 3 drawn balls are of the same colour is (JEE Adv. 2013)
PASSAGE - 4
A box B1 contains 1 white ball, 3 red balls and 2 black balls. Another box B2 contains 2 white balls, 3 red balls and 4 black balls. A third box B3 contains 3 white balls, 4 red balls and 5 black balls.
Q. If 2 balls are drawn (without replacement) from a randomly selected box and one of the balls is white and the other ball is red, the probability that these 2 balls are drawn from box B2 is
PASSAGE - 5
Box 1 contains three cards bearing numbers 1, 2, 3; box 2 contains five cards bearing numbers 1, 2, 3, 4, 5; and box 3 contains seven cards bearing numbers 1, 2, 3, 4, 5, 6, 7. A card is drawn from each of the boxes. Let xi be number on the card drawn from the ith box, i = 1, 2, 3. (JEE Adv. 2014)
Q. The probability that x1 + x2 + x3 is odd, is
PASSAGE - 5
Box 1 contains three cards bearing numbers 1, 2, 3; box 2 contains five cards bearing numbers 1, 2, 3, 4, 5; and box 3 contains seven cards bearing numbers 1, 2, 3, 4, 5, 6, 7. A card is drawn from each of the boxes. Let xi be number on the card drawn from the ith box, i = 1, 2, 3. (JEE Adv. 2014)
Q. 12. The probability that x1, x2, x3 are in an arithmetic progression, is
PASSAGE - 6
Let n1 and n2 be the number of red and black balls, respectively, in box I. Let n3 and n4 be the number of red and black balls, respectively, in box II. (JEE Adv. 2015)
Q. One of the two boxes, box I and box II, was selected at random and a ball was drawn randomly out of this box. The ball was found to be red. If the probability that this red ball was drawn from box II is 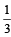 , then the correct option(s) with the possible values of n1, n2, n3 and n4 is(are)
, then the correct option(s) with the possible values of n1, n2, n3 and n4 is(are)
PASSAGE - 6
Let n1 and n2 be the number of red and black balls, respectively, in box I. Let n3 and n4 be the number of red and black balls, respectively, in box II. (JEE Adv. 2015)
Q. A ball is drawn at random from box I and transferred to box II. If the probability of drawing a red ball from box I, after this transfer, is 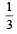 , then the correct option(s) with the possible values of n1 and n2 is(are)
, then the correct option(s) with the possible values of n1 and n2 is(are)
PASSAGE - 7
Football teams T1 and T2 have to play two games against each other. It is assumed that the outcomes of the two games are independent. The probabilities of T1 winning, drawing and losing a game against T2 are 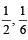 and
and 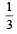 respectively. Each team gets 3 points for a win, 1 point for a draw and 0 point for a loss in a game.
respectively. Each team gets 3 points for a win, 1 point for a draw and 0 point for a loss in a game.
Let X and Y denote the total points scored by teams T1 and T2 respectively after two games.
Q.P (X > Y) is (JEE Adv. 2016)
PASSAGE - 7
Football teams T1 and T2 have to play two games against each other. It is assumed that the outcomes of the two games are independent. The probabilities of T1 winning, drawing and losing a game against T2 are 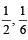 and
and 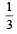 respectively. Each team gets 3 points for a win, 1 point for a draw and 0 point for a loss in a game.
respectively. Each team gets 3 points for a win, 1 point for a draw and 0 point for a loss in a game.
Let X and Y denote the total points scored by teams T1 and T2 respectively after two games.
Q. P (X = Y) is (JEE Adv. 2016)
|
347 docs|185 tests
|
|
347 docs|185 tests
|


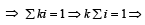
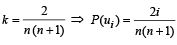
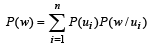
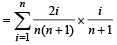
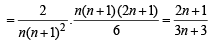
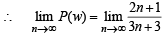
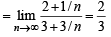
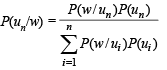
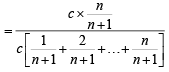
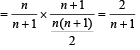
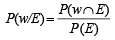
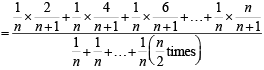
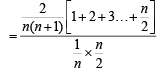 (n being even)
(n being even)