Test: Comprehension Based Questions: Vector Algebra and Three Dimensional Geometry - JEE MCQ
6 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: Comprehension Based Questions: Vector Algebra and Three Dimensional Geometry
Consider the lines
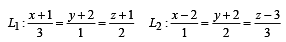
Q. The unit vector perpendicular to both L1 and L2 is
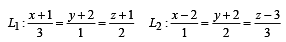
Consider the lines
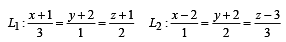
Q. The shortest distance between L1 and L2 is
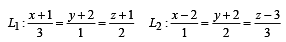
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider the lines
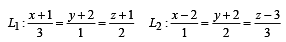
Q. The distance of the point (1, 1, 1) from the plane passing through the point (–1, –2, –1) and whose normal is perpendicular to both the lines L1 and L2 is
Consider the planes 3x – 6y – 2z = 15 and 2x + y – 2z = 5.
STATEMENT-1 : The parametric equations of the line of intersection of the given planes are x = 3 + 14t, y = 1 + 2t, z = 15t. because
STATEMENT-2 : The vector  is parallel to the line of intersection of given planes.
is parallel to the line of intersection of given planes.
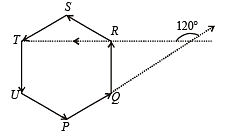
Let the vectors  epresent the sides of a regular hexagon.
epresent the sides of a regular hexagon.
STATEMENT-1 : 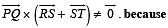
STATEMENT-2 : 
Consider three planes
P1 : x – y + z = 1
P2 : x + y – z = 1
P3 : x – 3y + 3z = 2
Let L1, L2, L3 be the lines of intersection of the planes P2 and P3, P3 and P1, P1 and P2, respectively.
STATEMENT - 1Z : At least two of the lines L1, L2 and L3 are non-parallel and
STATEMENT - 2 : The three planes doe not have a common point.
|
347 docs|185 tests
|
|
347 docs|185 tests
|



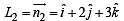


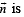
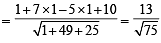
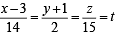



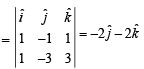
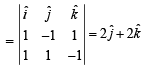
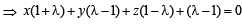
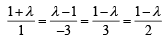 ...(1)
...(1)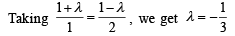 and taking
and taking