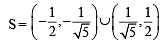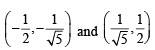Test: MCQs (One or More Correct Option): Quadratic Equation and Inequations (Inequalities) | JEE Advanced - JEE MCQ
9 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: MCQs (One or More Correct Option): Quadratic Equation and Inequations (Inequalities) | JEE Advanced
For real x, the function 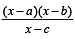 will assume all realvalues provided (1984 - 3 Marks)
will assume all realvalues provided (1984 - 3 Marks)
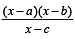 will assume all realvalues provided (1984 - 3 Marks)
will assume all realvalues provided (1984 - 3 Marks)If S is the set of all real x such that  is positive,then S contains (1986 - 2 Marks)
is positive,then S contains (1986 - 2 Marks)
 is positive,then S contains (1986 - 2 Marks)
is positive,then S contains (1986 - 2 Marks)| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If a, b and c are distinct positive numbers, then the expression (b + c – a)(c + a – b)(a + b – c) – abc is (1986 - 2 Marks)
If a, b, c, d and p are distinct real numbers such that (a2 + b2 + c2)p2 – 2 (ab + bc + cd)p + (b2 + c2 + d2) ≤ 0 then a, b, c, d (1987 - 2 Marks)
The equation 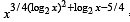
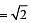 has
has
The product of n positive numbers is unity Then their sum is (1991 - 2 Marks)
Number of divisor of the form 4n + 2 (n ≥ 0) of the integer 240 is (1998 - 2 Marks)
If 3x = 4x–1, then x = (JEE Adv. 2013)
Let S be the set of all non-zero real numbers α such that the quadratic equation αx2 – x + α = 0 has two distinct real roots x1 and x2 satisfying the inequality |x1 – x2| < 1. Which of the following intervals is(are) a subset(s) of S? (JEE Adv. 2015)
|
327 docs|185 tests
|
|
327 docs|185 tests
|


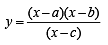
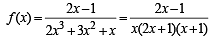
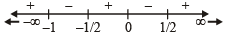


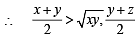
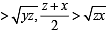
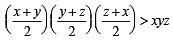
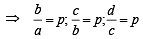
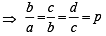
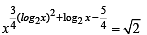 For x > 0, taking log on both sides to the base x, we get
For x > 0, taking log on both sides to the base x, we get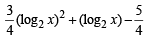
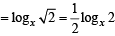
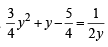
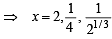 (All accepted as > 0)
(All accepted as > 0)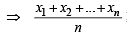
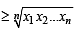
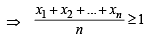 [Using eq. (1)]
[Using eq. (1)]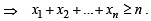
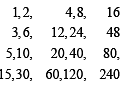
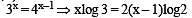
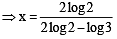
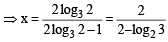
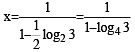
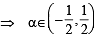 ...(i)
...(i)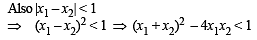
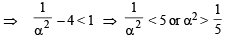
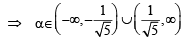 ...(ii)
...(ii)