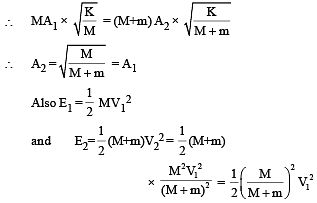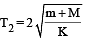Test: MCQs (One or More Correct Option): Simple Harmonic Motion (Oscillations) | JEE Advanced - JEE MCQ
11 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: MCQs (One or More Correct Option): Simple Harmonic Motion (Oscillations) | JEE Advanced
A particle executes simple harmonic motion with a frequency. f. The frequency with which its kinetic energy oscillates is
A linear harmonic oscillator of force constant 2 × 106 N/m and amplitude 0.01 m has a total mechanical energy of 160 J.
Its
Its
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A uniform cylinder of length L and mass M having cross sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half- submerged in a liquid of density ρ at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is k, the frequency of oscillation of the cylinder is
A highly rigid cubical block A of small mass M and side L is fixed rigidly on to another cubical block B of the same dimensions and of low modulus of rigidity η such that the lower face of A completely covers the upper face of B. The lower face of B is rigidly held on a horizontal surface. A small force F is applied perpendicular to one of the sides faces of A. After the force is withdrawn, block A executes small oscillations the time period of which is given by
One end of a long metallic wire of length L is tied to the ceiling. The other end is tied to a massless spring of spring constant K.A mass m hangs freely from the free end of the spring. The area of cross-section and the Young’s modulus of the wire are A and Y respectively. If the mass is slightly pulled down and released, it will oscillate with a time period T equal to:
A particle of mass m is executing oscillations about the origin on the x axis. Its potential energy is V(x) = k | x |3 where k is a positive constant. If the amplitude of oscillation is a, then its time period T is
Three simple harmonic motions in the same direction having the same amplitude a and same period are superposed. If each differs in phase from the next by 45°, then.
The function x = A sin2 ωt + B cos2 ωt + C sin ωt cosωt represent SHM for which of the option(s)
A metal rod of length ‘L’ and mass ‘m’ is pivoted at one end.
A thin disc of mass ‘M’ and radius ‘R’ (<L) is attached at its center to the free end of the rod. Consider two ways the disc is attached: (case A). The disc is not free to rotate about its centre and (case B) the disc is free to rotate about its centre.
The rod disc system performs SHM in vertical plane after being released from the same displaced position. Which of the following statement(s) is (are) true?
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies ω1 and ω2 and have total energies E1 and E2, respectively. The variations of their momenta p with positions x are shown in the figures.  then the correct equation(s) is(are)
then the correct equation(s) is(are)

A block with mass M is conn ected by a massless spring with stiffness constant k to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position x0. Consider two cases: (i) when the block is at x0; and (ii) when the block is at x = x0 + A. In both the cases, a particle with mass m(<M) is softly placed on the block after which they stick to each other. Which of the following statement(s) is (are) true about the motion after the mass m is placed on the mass M?
|
347 docs|185 tests
|
|
347 docs|185 tests
|












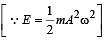
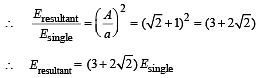






 ∴ B is a correct option.
∴ B is a correct option.