Test: MCQs (One or More Correct Option): Trigonometric Functions & Equations | JEE Advanced - JEE MCQ
14 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: MCQs (One or More Correct Option): Trigonometric Functions & Equations | JEE Advanced

 is equal to (1984 )
is equal to (1984 )

 is equal to (1984 )
is equal to (1984 )The expression 3  -
-  is equal to
is equal to
 -
-  is equal to
is equal to| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The number of all possible triplets (a1, a2, a3) such that a1 + a2 cos(2x) + a3sin2(x) = 0 for all x is (1987 - 2 Marks)
The values of θ lying between θ = 0 and θ = π/2 and satisfying the equation (1988 - 2 Marks)
 = 0 are
= 0 are
Let 2sin2x + 3sinx – 2 > 0 and x2 – x – 2 < 0 (x is measured in radians). Then x lies in the interval (1994)
The minimum value of the expression sin α + sin β + sin γ , where α, β, γ are real numbers satisfying α + β + γ = π is
The number of values of x in the interval [0, 5π] satisfying the equation 3 sin2 x – 7 sin x + 2 = 0 is (1998 - 2 Marks)
Which of the following number(s) is/are rational? (1998 - 2 Marks)
For a positive integer n, let (1999 - 3 Marks) 
 Then
Then
If  then (2009)
then (2009)
For 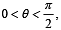 the solution (s) of
the solution (s) of 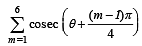
 is (are)
is (are)
(2009)
Let  be such that
be such that 


 then φ cannot satisfy (2012)
then φ cannot satisfy (2012)
The number of points in  for which x2 – x sin x – cos x = 0, is (JEE Adv. 2013)
for which x2 – x sin x – cos x = 0, is (JEE Adv. 2013)
Let f(x) = x sin πx, x > 0. Then for all natural numbers n, f'(x) vanishes at (JEE Adv. 2013)
|
347 docs|185 tests
|
|
347 docs|185 tests
|

















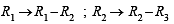


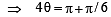
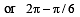








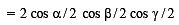
 lies between –1
lies between –1


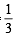 from the following graph is 6 between [0, 5π]
from the following graph is 6 between [0, 5π] (irrational)
(irrational) (irrational)
(irrational) (2 sin 15° cos 15°)
(2 sin 15° cos 15°)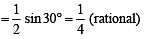
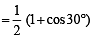
 (irrational)
(irrational)
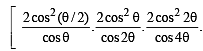

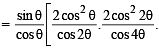

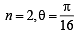




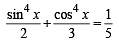




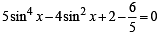
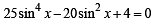
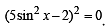




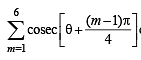



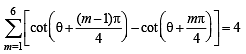





















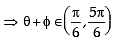
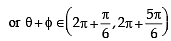


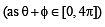
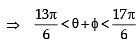




 and decreasing on
and decreasing on