Test: JEE Main 35 Year PYQs- Permutations & Combinations - JEE MCQ
22 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - Test: JEE Main 35 Year PYQs- Permutations & Combinations
Total number of four digit odd numbers that can be formed using 0, 1, 2, 3, 5, 7 (using repetition allowed) are [2002]
Number greater than 1000 but less than 4000 is formed using the digits 0, 1, 2, 3, 4 (repetition allowed). Their number is [2002]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Five digit number divisible by 3 is formed using 0, 1, 2, 3, 4 and 5 without repetition. Total number of such numbers are [2002]
The sum of integers from 1 to 100 that are divisible by 2 or 5 is[2002]
If nCr denotes the number of combination of n things taken r at a time, then the expression nCr +1 + nC r -1 + 2 x nCr equals[2003]
A student is to answer 10 out of 13 questions in an examination such that he must choose at least 4 from the first five questions. The number of choices available to him is[2003]
The number of ways in which 6 men and 5 women can dine at a round table if no two women are to sit together is given by[2003]
How many ways are there to arrange the letters in the word GARDEN with vowels in alphabetical order [2004]
The number of ways of distributing 8 identical balls in 3 distinct boxes so that none of the boxes is empty is [2004]
If the letters of the word SACHIN are arranged in all possible ways and these words are written out as in dictionary, then the word SACHIN appears at serial number [2005]
At an election , a voter may vote for an y number of candidates, not greater than the number to be elected. There are 10 candidates and 4 are of be selected, if a voter votes for at least one candidate, then the number of ways in which he can vote is [2006]
The set S = {1, 2, 3, ......., 12} is to be partitioned into three sets A , B, C of equal size. Thus A ∪ B ∪ C = S , A∩B =B∩C= A∩C= φ. The number of ways to partition S is [2007]
In a shop there are five types of ice-creams available. A child buys six ice-creams.Statement-1 : The number of different ways the child can buy the six ice-creams is 10C5.Statement -2 : The number of different ways the child can buy the six ice-creams is equal to the number of different ways of arranging 6 A’s and 4 B’s in a row. [2008]
How many different words can be formed by jumbling the letters in the word MISSISSIPPI in which no two S are adjacent?
From 6 different novels and 3 different dictionaries,4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. Then the number of such arrangement is: [2009]
There are two urns. Urn A has 3 distinct red balls and urn B has 9 distinct blue balls. From each urn two balls are taken out at random and then transferred to the other. The number of ways in which this can be done is [2010]
Statement-1: The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is 9C3 .Statement-2: The number of ways of choosing any 3 places from 9 different places is 9C3 . [2011]
These are 10 points in a plane, out of these 6 are collinear, if N is the number of triangles formed by joining these points. then:[2012]
Assuming the balls to be identical except for difference in colours, the number of ways in which one or more balls can be selected from 10 white, 9 green and 7 black balls is : [2012]
Let Tn be the number of all possible triangles formed by joining vertices of an n-sided regular polygon. If Tn+1 – Tn = 10, then the value of n is : [JEE M 2013]
The number of integers greater than 6,000 that can be formed, using the digits 3, 5, 6, 7 and 8, without repetition, is : [JEE M 2015]
If all the words (with or without meaning) having five letters, formed using the letters of the word SMALL and arranged as in a dictionary; then the position of the word SMALL is : [JEE M 2016]
|
447 docs|930 tests
|
|
447 docs|930 tests
|


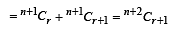
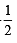 x 720 = 360
x 720 = 360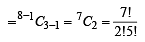
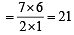
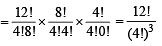
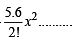
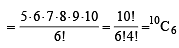
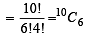 which is same as the number of ways the child can buy six icecreams.
which is same as the number of ways the child can buy six icecreams. ways
ways

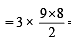 = 3 x 36 = 108
= 3 x 36 = 108 = 120 - 20 =100
= 120 - 20 =100