Test: Comprehension Based Questions: Matrices and Determinants - JEE MCQ
13 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: Comprehension Based Questions: Matrices and Determinants
A square matrix in which all the elements except at least the one element in the diagonal are zeros is said to be a
PASSAGE - 1
 and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying
and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying 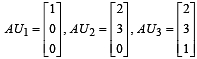 evaluate as directed in the following questions
evaluate as directed in the following questions
Q. The sum of the elements of the matrix U–1 is
 and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying
and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying 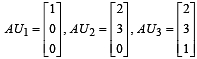 evaluate as directed in the following questions
evaluate as directed in the following questions| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
PASSAGE - 1
 and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying
and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying 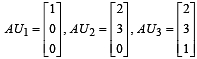 evaluate as directed in the following questions
evaluate as directed in the following questions
Q. The value of 
 and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying
and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying 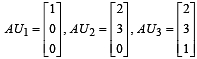 evaluate as directed in the following questions
evaluate as directed in the following questions
PASSAGE - 2
Let 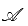 be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
Q. The number of matrices in 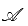 is
is
PASSAGE - 2
Let 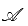 be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
Q. The number of matrices A in 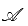 for which the system of linear equations
for which the system of linear equations
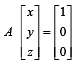
PASSAGE - 2
Let 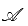 be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
Q. The number of matrices A in 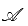 for which the system of linear equations
for which the system of linear equations

PASSAGE - 3
Let p be an odd prime number and Tp be the following set of 2 × 2 matrices :

Q. The number of A in Tp such that A is either symmetric or skew-symmetric or both, and det(A) divisible by p is
PASSAGE - 3
Let p be an odd prime number and Tp be the following set of 2 × 2 matrices :

Q. The number of A in Tp such that the trace of A is not divisible by p but det (A) is divisible by p is
[Note: The trace of a matrix is the sum of its diagonal entries.]
PASSAGE - 3
Let p be an odd prime number and Tp be the following set of 2 × 2 matrices :

Q. The number of A in Tp such that det (A) is not divisible by p is
PASSAGE - 4
Let a, b and c be three real numbers satisfying
 ...(E)
...(E)
Q. If the point P(a, b, c), with reference to (E), lies on the plan e 2x + y + z = 1, then the value of 7a + b + c is
PASSAGE - 4
Let a, b and c be three real numbers satisfying
 ...(E)
...(E)
Q. Let ω be a solution of x3 – 1 = 0 with Im (ω) > 0 , if a = 2 with b and c satisfying (E), then the value of  equal to
equal to
PASSAGE - 4
Let a, b and c be three real numbers satisfying
 ...(E)
...(E)
Q. Let b = 6, with a and c satisfying (E). If a and b are the roots of the quadratic equation ax2 + bx + c = 0, then 
Consider the system of equations
x – 2y + 3z = –1
–x + y – 2z = k
x – 3y + 4z = 1
STATEMENT - 1 : The system of equations has no solution for k ¹ 3 and
STATEMENT-2 : The determinant  k ≠ 3 .
k ≠ 3 .
|
327 docs|185 tests
|
|
327 docs|185 tests
|


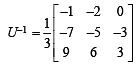

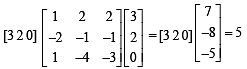
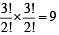


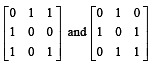


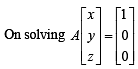
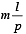 then on dividing bc by p we should get
then on dividing bc by p we should get  for some
for some



















