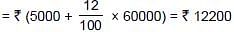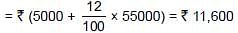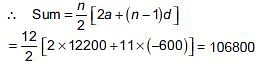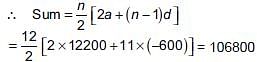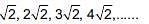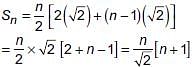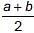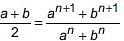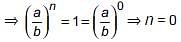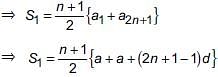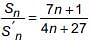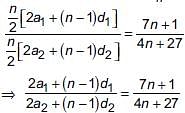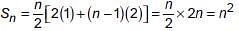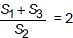Math Olympiad Test: Arithmetic Progression- 4 - Class 10 MCQ
10 Questions MCQ Test Olympiad Preparation for Class 10 - Math Olympiad Test: Arithmetic Progression- 4
Deepak repays his total loan of ₹1,18,000 by paying every month starting with the first instalment of ₹1000. If he increases the instalment by ₹100 every month. what amount will be paid as the last instalment of loan?
The production of TV in a factory increases uniformly by a fixed number every year. It produced 8000 sets in 6th year and 11300 in 9th year. Find the production in the 6 years.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Raghav buys a shop for ₹ 120000. He pays half of the amount in cash and agrees to pay the balance in 12 annual instalments of ₹ 5000 each. If the rate of interest is 12% and he pays the interest due on the unpaid amount with the instalment. Find the total cost of the shop.
A manufacturer of laptop produced 6000 units in 3rd year and 7000 units in the 7th year. Assuming that production increases uniformly by a fixed number every year, find the production in the 5th year.
Which of the following statements is INCORRECT?
(a) Sum of n terms of the list of numbers 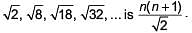
(b) The common difference of the A.P. given by an = 3n + 2 is 3.
(c) The sum of the A.P. (–5), (–8), (–11), ..., (–230) is –8930.
There are 25 trees at equal distances of 5 metres in a line with a well, the distance of the well from the nearest tree being 10 metres. A gardener waters all the trees separately starting from the well and he returns to the well after watering each tree to get water for the next. Find the total distance the gardner will cover in order to water all the trees.
If  is the A.M. between a and b, then find the value of n.
is the A.M. between a and b, then find the value of n.
If there are (2n + 1) terms in A.P., then find the ratio of the sum of odd terms and the sum of even terms.
Fill in the blanks.
(i) If the ratio of sum of n terms of two A.P. is (7n + 1) : (4n + 27), then ratio of their mth terms is P.
(ii) Sum of n odd natural numbers is Q.
(iii) If sum of n terms of three A.P. are S1, S2, S3. The first term of each is 1 and common differance are 1, 2 and 3 respectively, then 
The sum of the third and seventh terms of an A.P. is 6 and their product is 8. Find the sum of first sixteen terms of the A.P.
|
13 videos|44 docs|187 tests
|
|
13 videos|44 docs|187 tests
|