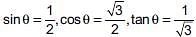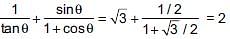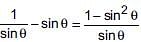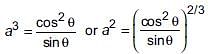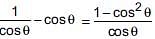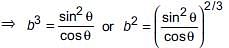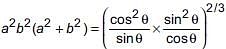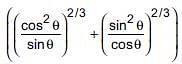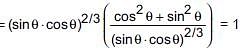Math Olympiad Test: Trigonometry- 4 - Class 10 MCQ
10 Questions MCQ Test Olympiad Preparation for Class 10 - Math Olympiad Test: Trigonometry- 4
If X sin3θ + Y cos3θ = sinθ cosθ and Xsinθ = Ycosθ, then
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If sin x + sin2x = 1, then cos8 x + 2cos6x + cos4x =_____.
If cosecθ – sinθ = l and sec θ– cosθ = m, then l2m2(l2 + m2 + 3) = ________ .
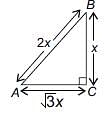
In a ΔABC, it is given that ∠C = 90° and tan A = 1/√3, find the value of (sinA cosB + cosA sinB).
Which of the following is true?
(a) cosθsinθ - 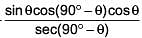
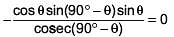
(b) If A and B are complementary angles, then sin A = 
Fill in the blanks.
(i) If x = a cos3θ , y = b sin3θ then 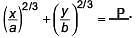
(ii) If x = a secθ cosφ, y = b secθ sinφ and z = c tanφ, then 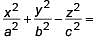
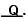
(iii) If cosA + cos2A = 1, then sin2A + sin4A 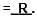
Which of the following is CORRECT statements?
(i) 3(sinθ – cosθ)4 + 6(sinθ + cosθ)2 + 4(sin6θ + cos6θ) is independent of θ.
(ii) If cosecθ – sinθ = a3, secθ – cosθ = b3, then a2b2(a2 + b2) = 2
|
13 videos|44 docs|187 tests
|
|
13 videos|44 docs|187 tests
|


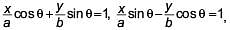 then _________.
then _________.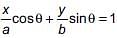 ... (i)
... (i)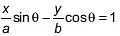 ... (ii)
... (ii)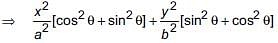
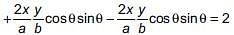
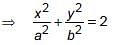
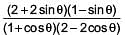
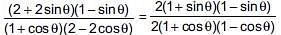

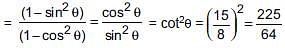
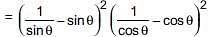
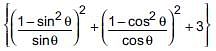
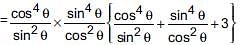
 and sin B =
and sin B = 
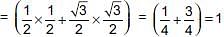
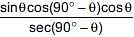


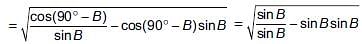
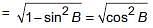

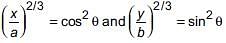
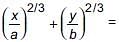 cos2θ + sin2θ = 1
cos2θ + sin2θ = 1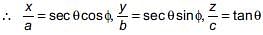
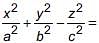 (secθ cosφ)2 + (secθ sinφ)2 – (tanθ)2
(secθ cosφ)2 + (secθ sinφ)2 – (tanθ)2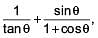 if 1 + cot2θ =
if 1 + cot2θ =