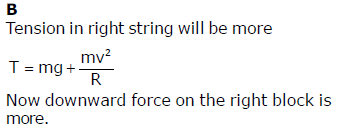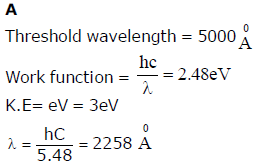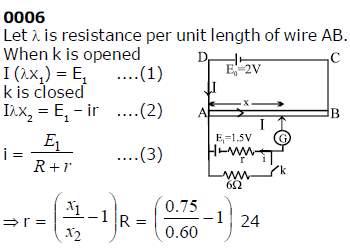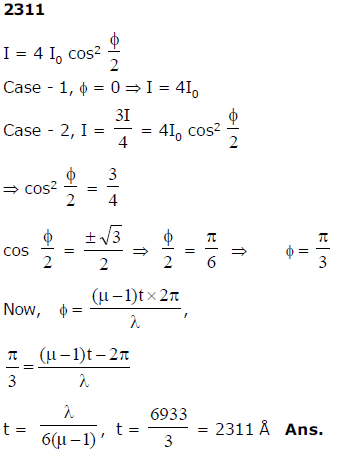JEE Advanced Test- 15 - JEE MCQ
30 Questions MCQ Test Mock Tests for JEE Main and Advanced 2025 - JEE Advanced Test- 15
Two identical conducting balls A and B have positive charges q1 and q2 respectively. But q1 ≠ q2. The balls are brought together so that they touch each other and then kept in their original positions. The force between them is ______.
How many 6mF, 200 V condensers are needed to make a condenser of 18 pF, 600 V?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A closed organ pipe and an open organ pipe of same length produce 2 beats/second while vibrating in their fundamental modes. The length of the open organ pipe is halved and that of closed pipe is doubled. Then, the number of beats produced per second while vibrating in the fundamental mode is ______.
A current of 5A is flowing at 220 V in the primary coil of a transformer. If the voltage produced in the secondary coil is 2200 V and 50% of power is lost, then the current in the secondary will be
A convex lens of focal length 30 cm produces 5 times magnified real image of an object. What is the object distance?
In a series resonant R-L-C circuit, the voltage across R is 100 V and the value of R = 1000 W. The capacitance of the capacitor is 2 ´ 10-6 F; angular frequency of AC is 200 rad s-1. Then the P.D. across the inductance coil is ______.
There is a uniform magnetic field directed perpendicular and into the plane of the paper. An irregular shaped conducting loop is slowly changing into a circular loop in the plane of the paper. Then ______.
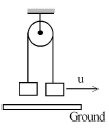
Two equal masses hang on either side of a pulley at the same height from the ground. The mass on the right is given a horizontal speed, after some time.
A metallic surface is irradiated with monochromatic light of variable wavelength. Above a wavelength of 5000 Å, no photoelectrons are emitted from the surface. With an unknown wavelength, a stopping potential of 3V is necessary to eliminate the photo current. The unknown wavelength is
Three liquids of equal masses are taken in three identical cubical vessels A, B and C. Their densities are PA, PB and PC respectively. But PA < PB < PC. The force exerted by the liquid on the base of the cubical vessel is ______
Two identical conducting balls A and B have positive charges q1 and q2 respectively. But q1 ≠ q2. The balls are brought together so that they touch each other and then kept in their original positions. The force between them is ______.
Two tangent galvanometers A and B are identical except in their number of turns. They are connected in series. On passing a current through them, deflections of 600 and 300 are produced. The ratio of the number of turns in A and B is
Water is in streamline flow along a horizontal pipe with nonuniform cross-section. At a point in the pipe where the area of cross-section is 10 cm2, the velocity of water is 1 ms-1 and the pressure is 2000 Pa. The pressure at another point where the cross-sectional area is 5 cm2 is ______.
A vertical capillary tube with inside radius 0.25 mm is submerged into water so that the length of its part over the water surface is equal to 25 mm. Surface tension of water is 73x10-3 N/m and angle of contact is zero degree for glass and water, acceleration due to gravity is 9.8 m/s2. Then choose correct statement.
Where R is radius of meniscus and h is height of water in capillary tube.
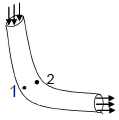
Ideal fluid flows along a atube of uniform cross section, located in a horizontal plane and bent as shown in figure. The flow is steady, 1 and 2 are two points in the tube. If P1 and P2 are pressure at the two points and v1 and v2 are the respective velocities, given that point 1 and 2 are at nearly same vertical level
Four wires of equal length 2m are arranged as shown in the figure. Wires 2, 3 and 4 are of equal cross sectional area and wire 1 is of half the cross section of these wires. By how much distance pointer at point 5 must be moved to get null point in cm ?
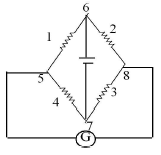
For the arrangement of the potentiometer shown in the figure, the balance point is obtained at a distance 75 cm from A when the key k is open.The second balance point is obtained at 60 cm from A when the key k is closed. Find the internal resistance (in ?) of the battery E1.
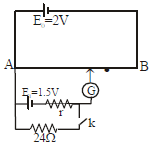
A cylinder fitted with a spring loaded piston shown in figure contains 0.01m3 gas at a pressure of 105 Pa. The cross-sectional area of the piston is 0.05 m2. Initially the spring does not touch the piston but atmospheric pressure of 105 Pa acts on the piston. The gas is slowly heated till the volume is increased to three times the original value. If the force constant of the spring is 25 kN / m, calculate the work done (in Joule) by the gas.
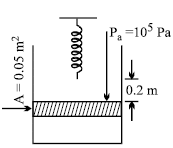
The intensity received at the focus of the lens is I when no glass slab has been placed in front of the slit. Both the slits are of the same dimension and the plane wavefront incident perpendicularly on them, has wavelength λ. On placing the glass slab, the intensity reduces to 3I/4 at the focus. Find out the minimum thickness of the glass slab (in Å) if its refractive index is 3/2. Given λ = 6933Å, µ = 1.5.
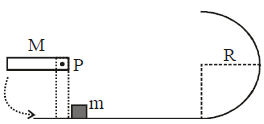
A rod of length R and mass M is free to rotate about a horizontal axis passing through hinge P as shown in the figure. First it is taken aside such that it becomes horizontal and then released. At the lowest point the rod hits the block B of mass m and stops. If mass of rod is (√60) kg, find mass of the block if it just complete the circle.
Which among the following factors is the most important in making fluorine the strongest oxidizing halogen
The standard electrode potential for the half cell reactions are:
Zn++ + 2e– → Zn E° = – 0.76 V
Fe++ + 2e– → Fe E° = – 0.44 V
The E.M.F. of the cell reaction :
Fe++ + Zn → Zn++ +Fe is
An elemental crystal has a density of 8570 kg m–3. The packing efficiency is 0.68. If the closest distance between neighbouring atoms is 2.86 Å, the mass of one atom is(1 amu=1.66×10–27 kg)
The value of DH for the reaction
X2g + 4Y2(g) Ý 2XY4(g) is less than zero. Formation of XY4(g) will be favoured at
The stabilization of a dispersed phase in a lyophobic colloid is due to:
Which of the following used is a promoter in Haber’s method to manufacture of ammonia
The ease of liquification and polarizibility of noble gases decreases in the order
For a reversible reaction : X(g) + 3Y(g) ⇌ 2Z(g)DH = –40 kJ the standard entropies of X, Y and Z arc 60, 40 and 50 JK–1 mol–1 respectively.The temperature at which the above reaction attains equilibrium is about
The rate constant, the activation energy, and the Arrhenius parameter of a chemical reaction at 25°C are 3.0×10–4 s–1 104.4 kJ mol–1, and 6.0 × 1014 s–1, respectively. The value of the rate constant as T → ∞ is
|
357 docs|148 tests
|
|
357 docs|148 tests
|