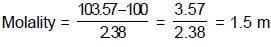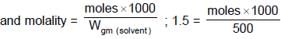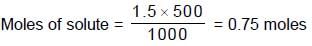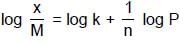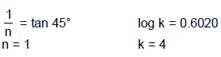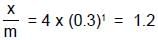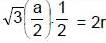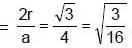JEE Advanced Test- 2 - JEE MCQ
30 Questions MCQ Test Mock Tests for JEE Main and Advanced 2025 - JEE Advanced Test- 2
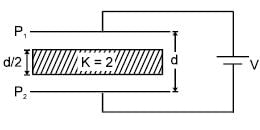
In the figure shown a parallel plate capacitor has a dielectric of width d/2 and dielectric constant K = 2. The other dimensions of the dielectric are same as that of the plates. The plates P1 and P2 of the capacitor have area 'A' each. The energy of the capacitor is :

A rod of length l having uniformly distributed charge Q is rotated about one end with constant frequency ' f '. Its magnetic moment.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Two identical spheres of same mass and specific gravity (which is the ratio of density of a substance and density of water) 2.4 have different charges of Q and – 3Q. They are suspended from two strings of same length l fixed to points at the same horizontal level, but distant l from each other. When the entire set up is transferred inside a liquid of specific gravity 0.8, it is observed that the inclination of each string in equilibrium remains unchanged. Then the dielectric constant of the liquid is
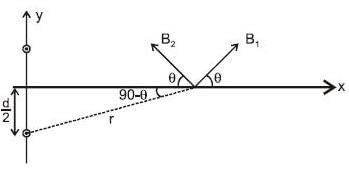
Two infinitely long parallel wires are a distance d apart and carry equal parallel currents I in the same direction as shown in the figure. If the wires are located on y axis (normal to x-y plane) at y = d/2 and y = -d/2, then the magnitude of x-coordinate of the point on x-axis where the magnitude of magnetic field is maximum is (Consider points on x-axis only)
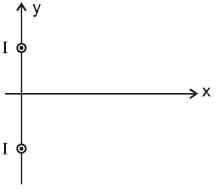
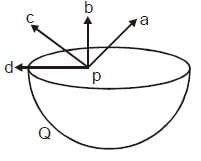
Figure shows a uniformly charged hemispherical shell. The direction of electric field at point p, that is off-centre (but in the plane of the largest circle of the hemisphere), will be along
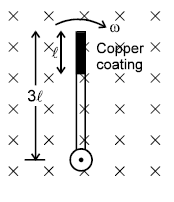
A wooden stick of length 3l is rotated about an end with constant angular velocity ω in a uniform magnetic field B perpendicular to the plane of motion. If the upper one third of its length in coated with copper, the potential difference across the copper coating of the stick is
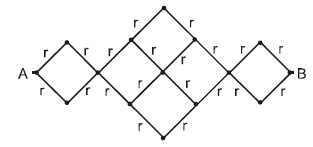
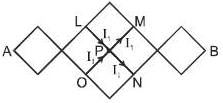
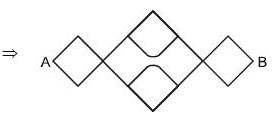
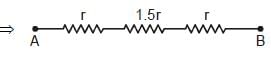
The resistance of each straight section is r. Find the equivalent resistance between A and B.
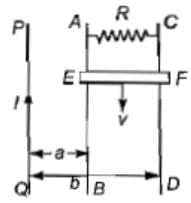
PQ is an infinite current carrying conductor. AB and CD are smooth conducting rods on which a conductor EF moves with constant velocity V as shown. The force needed to maintain constant speed of EF is.
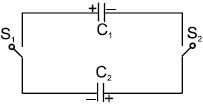
Two capacitors C1 & C2 are charged to same potential V, but with opposite polarity as shown in fig. The switch S1 & S2 are then closed.
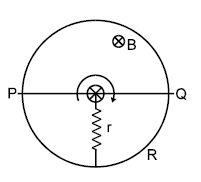
In the figure shown ‘R’ is a fixed conducting ring of negligible resistance and radius ‘a’. PQ is a uniform rod of resistance r. It is hinged at the centre of the ring and rotated about this point in clockwise direction with a uniform angular velocity ω. There is a uniform magnetic field of strength ‘B’ pointing inwards. ‘r’ is a stationary resistance, then choose correct statements
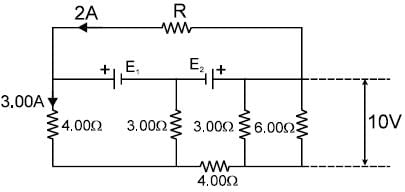
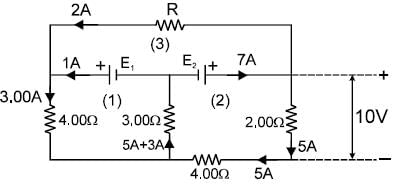
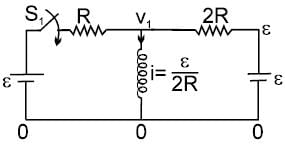
In the circuit shown in figure, E1 and E2 are two ideal sources of unknown emfs. Some currents are shown. Potential difference appearing across 6? resistance is VA – VB = 10V.
A proton of charge 'e' and mass 'm' enters a uniform and constant magnetic field with an initial velocity
Which of the following will be correct at any later time 't' :
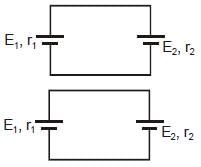
Satement-1 : Two cells of unequal emf E1 and E2 having internal resistances r1 and r2 are connected as shown in figure. Then the potential difference across any cell cannot be zero.
Satement-2 : If two cells having nonzero internal resistance and unequal emf are connected across each other as shown, then the current in the
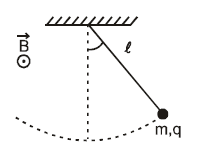
Satement-1 : A pendulum made of an insulated rigid massless rod of length l is attached to a small sphere of mass m and charge q. The pendulum is undergoing oscillations of small amplitude having time period T. Now a uniform horizontal magnetic field out of plane of page is switched on. As a result of this change, the time period of oscillations does not change.
Satement-2 : A force acting along the string on the bob of a simple pendulum (such that tension in string is never zero) does not produce any restoring torque on the bob about the hinge.
In the shown circuit involving a resistor of resistance R W, capacitor of capacitance C farad and an ideal cell of emf E volts, the capacitor is initially uncharged and the key is in position 1. At t = 0 second the key is pushed to position 2 for t0 = RC seconds and then key is pushed back to position 1 for t0 = RC seconds. This process is repeated again and again. Assume the time taken to push key from position 1 to 2 and vice versa to be negligible.
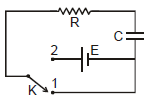
Q. The charge on capacitor at t = 2RC second is
In the shown circuit involving a resistor of resistance R W, capacitor of capacitance C farad and an ideal cell of emf E volts, the capacitor is initially uncharged and the key is in position 1. At t = 0 second the key is pushed to position 2 for t0 = RC seconds and then key is pushed back to position 1 for t0 = RC seconds. This process is repeated again and again. Assume the time taken to push key from position 1 to 2 and vice versa to be negligible.

Q. The current through the resistance at t = 1.5 RC seconds is
In the shown circuit involving a resistor of resistance R W, capacitor of capacitance C farad and an ideal cell of emf E volts, the capacitor is initially uncharged and the key is in position 1. At t = 0 second the key is pushed to position 2 for t0 = RC seconds and then key is pushed back to position 1 for t0 = RC seconds. This process is repeated again and again. Assume the time taken to push key from position 1 to 2 and vice versa to be negligible.

Q. Then the variation of charge on capacitor with time is best represented by
Matrix Match
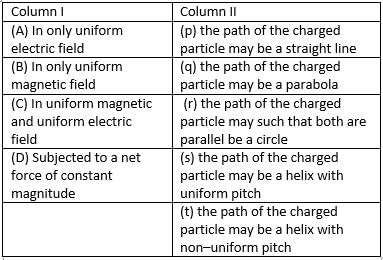
A charged particle having non zero velocity is subjected to certain conditions given in Column I . Column II gives possible trajectories of the particle. Match the conditions in column I with the results in Column II
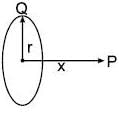
A uniformly charged ring of radius 0.1 m rotates at a frequency of 104 rps about its axis. The ratio of energy density of electric field to the energy density of the magnetic field at a point on the axis at distance 0.2 m from the centre is in form X × 109. Find the value of X. (Use speed of light c = 3 × 108 m/s, π2 = 10)
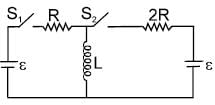
In the circuit shown S1 and S2 are switches. S2 remains closed for a long time and S1 open. Now S1 is also closed. It is given that R = 10Ω , L = 1 mH and ε = 3V. Just after S1 is closed, the magnitude of rate of change of current (in ampere/sec.) that is , in the inductor L is x × 102 A/s find x
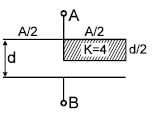
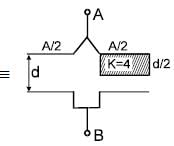
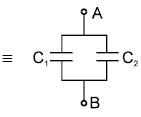
The equivalent capacitance between terminals ‘A’ and ‘B’ is Find x. The letters have their usual meaning.
The current density inside a long, solid, cylindrical wire of radius a = 12 mm is in the direction of the central axis and its magnitude varies linearly with radial distance r from the axis according to
where
A/m2. Find the magnitude of the magnetic field at r = a/2 in μT.
(half-life = 15 hrs.) is known to contain some radioactive impurity (half-life = 3 hrs.) in a sample. This sample has an initial activity of 1000 counts per minute, and after 30 hrs it shows an activity of 200 counts per minute. What percent of the initial activity was due to the impurity ?
For the cell (at 298 K)
Ag(s) | AgCl(s) | Cl– (aq) || AgNO3 (aq) | Ag(s)
Which of following is correct :
At 298K the standard free energy of formation of H2O(l) is –257.20 kJ/mole while that of its ionisation into H+ ions and OH– ions is 80.35 kJ/mole, then the emf of the following cell at 298 K will be (Take F = 96500 C] :
H2(g,1 bar) | H+ (1M) || OH¯ (1M) | O2 (g, 1bar)
Consider the reaction, NH2NO2 (aq) ———? N2O(g) + H2O(l)
The concentration of nitramide as a function of time is shown below for a particular run.
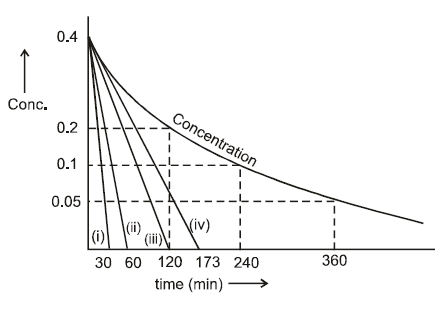
Which line represents the correct tangent to the graph at the origin (t = 0) ?
In a hypothetical reaction
A(aq) 2B(aq) + C(aq) (1st order decomposition)
'A' is optically active (dextro-rototory) while 'B' and 'C' are optically inactive but 'B' takes part in a titration reaction (fast reaction) with H2O2. Hence the progress of reaction can be monitored by measuring rotation of plane of plane polarised light or by measuring volume of H2O2 consumed in titration.
In an experiment the optical rotation was found to be θ = 40° at t = 20 min and θ = 10° at t = 50 min. from start of the reaction. If the progress would have been monitored by titration method, volume of H2O2 consumed at t = 15 min. (from start) is 40 ml then volume of H2O2 consumed at t = 60 min will be:
How many m.moles of sucrose should be dissolved in 500 grams of water so as to get a solution which has a difference of 103.57°C between boiling point and freezing point ?
(Kf = 1.86 K Kg mol–1, Kb = 0.52 K Kg mol–1)
When a graph is plotted between log x/m and log p, it is straight line with an angle 45° and intercept 0.6020 on y-axis. If initial pressure is 0.3 atm, what will be the amount of gas adsorbed per gram of adsorbent :
Diamond has face-centred cubic lattice. There are two atoms per lattice point, with the atoms at (000) and coordinates. The ratio of the carbon-carbon bond distance to the edge of the unit cell is:
|
357 docs|148 tests
|
|
357 docs|148 tests
|


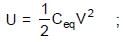
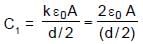

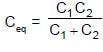

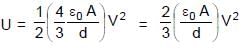

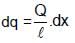
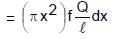
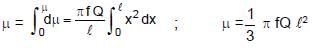
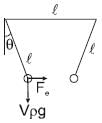
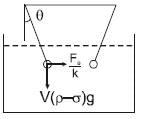
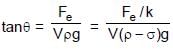 ⇒
⇒ 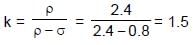
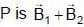 where
where  are magnetic field at P due to wire 1 and 2.
are magnetic field at P due to wire 1 and 2.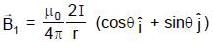

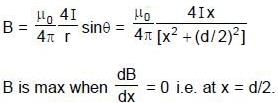
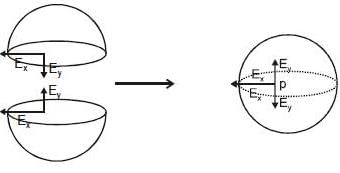
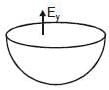

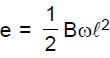

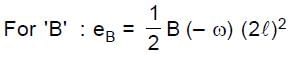 Resultant induced emf will be :
Resultant induced emf will be : 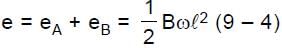
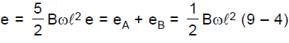
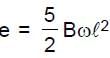

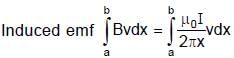
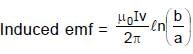 ⇒
⇒ 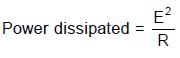
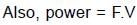 ⇒
⇒ 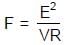
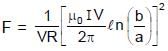
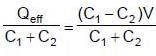
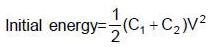
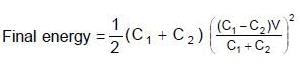
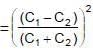
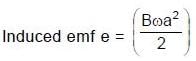 (∵ Radius = a)
(∵ Radius = a)
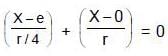

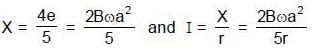
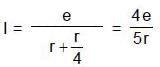
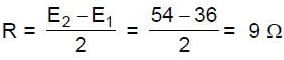
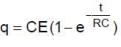
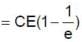
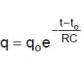 and
and 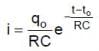
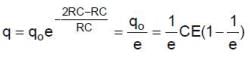
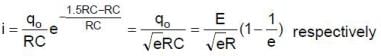
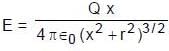
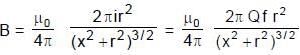
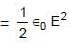 Magnetic energy density
Magnetic energy density 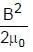
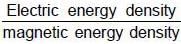
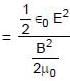
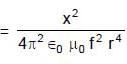
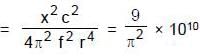
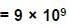

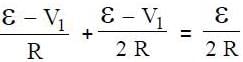
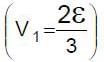
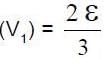


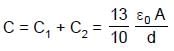
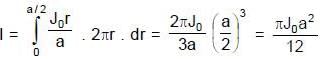
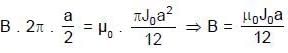
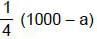 cpm
cpm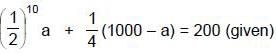
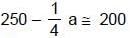
 ⇒ a = 200
⇒ a = 200 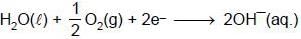

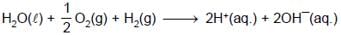
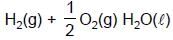
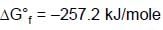
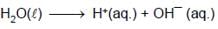
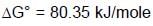
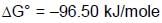
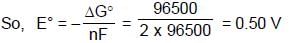
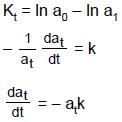
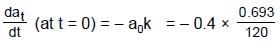
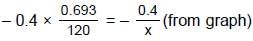
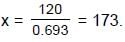
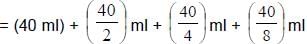 = 75 ml Ans.
= 75 ml Ans.