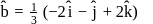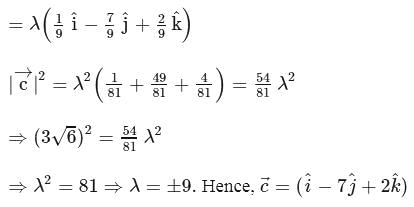Vector Algebra: Vector Addition(20 Nov) - JEE MCQ
10 Questions MCQ Test Daily Test for JEE Preparation - Vector Algebra: Vector Addition(20 Nov)
Let A(4, 7, 8), B(2, 3, 4) and C(2, 5, 7) be the position vectors of the vertices of a ∆ABC. The length of the internal bisector of the angle of A is
If  are three non-coplanar non-zero vectors, then
are three non-coplanar non-zero vectors, then 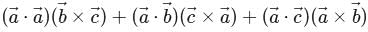 is equal to
is equal to
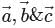 are three non-coplanar non-zero vectors, then
are three non-coplanar non-zero vectors, then 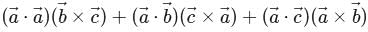 is equal to
is equal to| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If 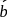 and
and 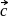 are any two non-collinear mutually perpendicular unit vectors and
are any two non-collinear mutually perpendicular unit vectors and 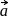 is any vector, then
is any vector, then 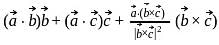 is equal to :
is equal to :
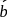 and
and 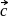 are any two non-collinear mutually perpendicular unit vectors and
are any two non-collinear mutually perpendicular unit vectors and 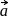 is any vector, then
is any vector, then 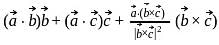 is equal to :
is equal to :If  and
and 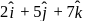 are the position vectors of the vertices A, B and C respectively of triangle
are the position vectors of the vertices A, B and C respectively of triangle 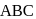 . The position vector of the point where the bisector of angle A meets
. The position vector of the point where the bisector of angle A meets 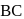 is:
is:
The vector that is parallel to the vector 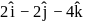 and coplanar with the vectors
and coplanar with the vectors 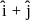 and
and 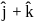 is
is
If  and
and  evaluate
evaluate 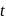 , if the vector
, if the vector 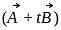 and
and  are mutually perpendicular.
are mutually perpendicular.
If three points A,B and C have position vectors (1, x, 3), (3, 4, 7) and (y, −2, −5) respectively and if they are collinear, then (x, y) is
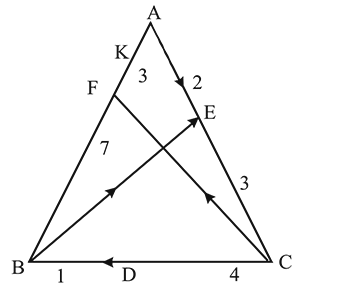
The points 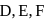 divide
divide  and
and 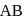 of the triangle
of the triangle 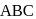 in the ratio
in the ratio 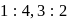 and
and 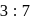 respectively and the point
respectively and the point 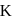 divides
divides 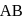 in the ratio
in the ratio 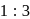 , then
, then  is equal to
is equal to
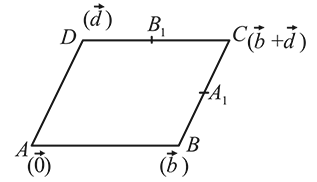
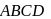 a parallelogram, and
a parallelogram, and 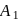 and
and 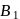 are the midpoints of sides
are the midpoints of sides  and
and  , respectively. If
, respectively. If 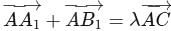 , then
, then 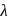 is equal to
is equal to
The vector 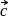 directed along the bisectors of the angle between the vectors
directed along the bisectors of the angle between the vectors 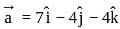 ,
, 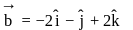 and
and 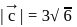 is given by
is given by
|
360 tests
|


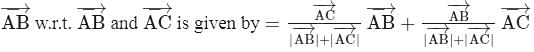
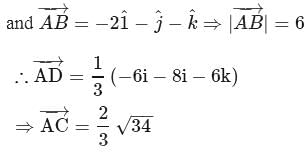
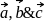 are non-coplanar
are non-coplanar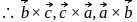 are also non-coplanar.
are also non-coplanar.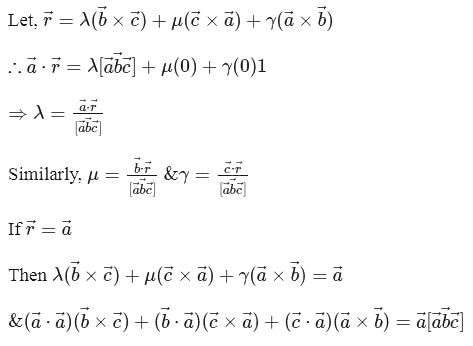
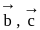 and
and 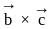 are mutually perpendicular vectors, therefore any vector
are mutually perpendicular vectors, therefore any vector 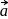 can be expressed in terms of
can be expressed in terms of 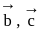 and
and 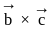
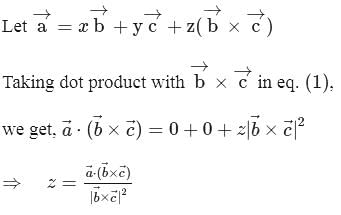
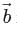 in eq. (1), we get
in eq. (1), we get 
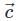 in eq. (1), we get
in eq. (1), we get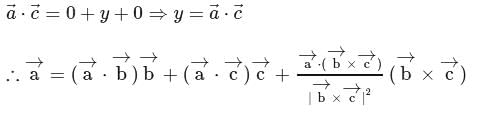
 be the origin and the bisector of
be the origin and the bisector of 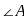 meets
meets 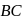 at
at 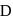 . Then
. Then 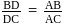 and position vector of
and position vector of  is given by
is given by

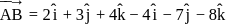
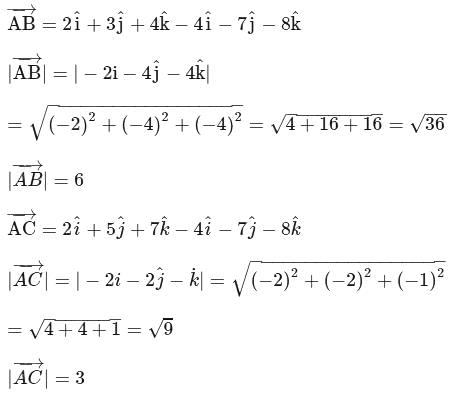

 .
.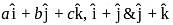
 are coplanar so one must be linear combination of other twoi.e,
are coplanar so one must be linear combination of other twoi.e,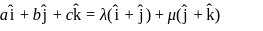
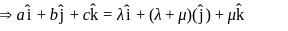
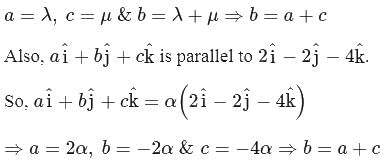
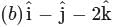 has a = 1, b = −1, c = −2 such that a + c = 1 − 2 = −1 = b ⇒ b = a + c
has a = 1, b = −1, c = −2 such that a + c = 1 − 2 = −1 = b ⇒ b = a + c
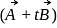 is perpendicular to
is perpendicular to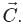
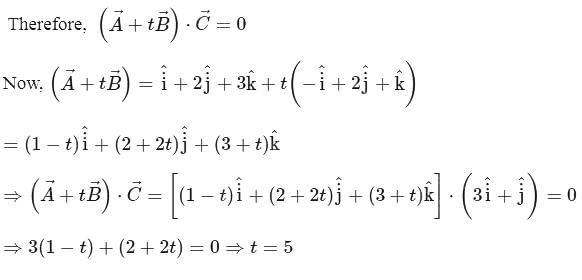
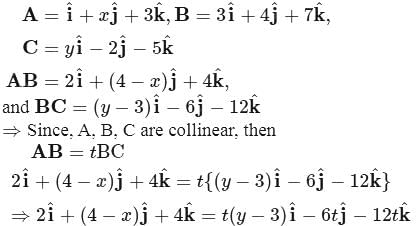
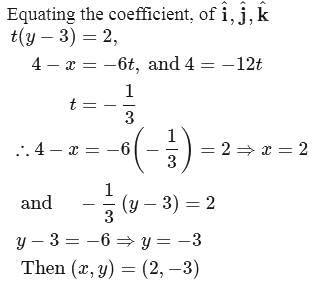
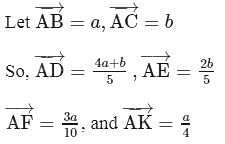
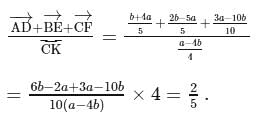
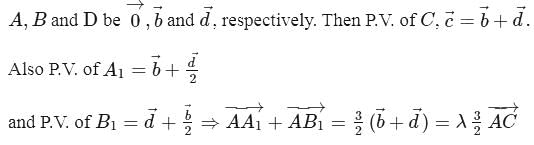


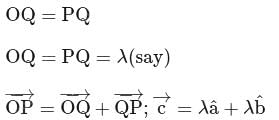
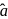 and
and 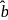 be unit
be unit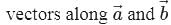 respectively, then
respectively, then 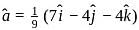 and
and