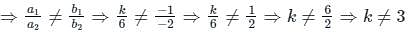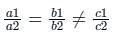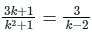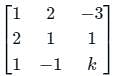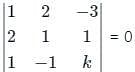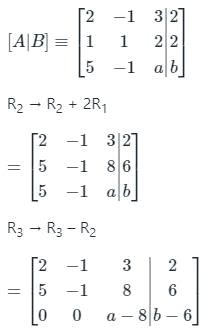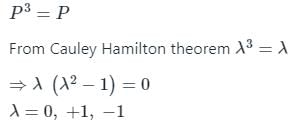Test: System of Linear Equations (May 6) - JEE MCQ
10 Questions MCQ Test Daily Test for JEE Preparation - Test: System of Linear Equations (May 6)
The nine numbers x1, x2, x3 ... x9, are in ascending order. Their average m is strictly greater than all the first eight numbers. Which of the following is true?
If a system of simultaneous equations has infinite solutions, then that system of equations is called:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let v1, . . . , v9 be the column vectors of a non-zero 9 × 9 real matrix A. Let a1, . . . , a9 ∈ ℝ, not all zero, be such that 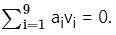 Then the system Ax =
Then the system Ax = 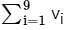 has
has
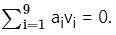 Then the system Ax =
Then the system Ax = 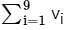 has
hasThe value of k for which the system of equations.
kx - y = 2
6x - 2y = 3
has a unique solution is
For what value of k, the system linear equation has no solution
(3k + 1)x + 3y - 2 = 0
(k2 + 1)x + (k - 2)y - 5 = 0
A set of linear equations is given in the form Ax = b, where A is a 2 × 4 matrix with real number entries and b ≠ 0. Will it be possible to solve for x and obtain a unique solution by multiplying both left and right sides of the equation by AT (the super script T denotes the transpose) and inverting the matrix AT A? Answer is
The value of k, for which the following system of linear equations has a non-trivial solution.
x + 2y - 3z = 0
2x + y + z = 0
x - y + kz = 0
The set of equations
x + y + z = 1
ax – ay + 3z = 5
5x – 3y + az = 6
has infinite solutions, if a =
If the system
2x – y + 3z = 2
x + y + 2z = 2
5x – y + az = b
Has infinitely many solutions, then the values of a and b, respectively, are
A 3 × 3 matrix is such that, P3 = P. Then the eigenvalues of P are
|
360 tests
|


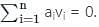
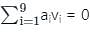 where all ���� are not zero Hence vectors are linearly dependent
where all ���� are not zero Hence vectors are linearly dependent  rank of A is less than 9 (number of column vectors )
rank of A is less than 9 (number of column vectors )