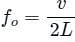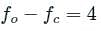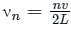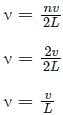Test: Standing Waves(17 Oct) - JEE MCQ
10 Questions MCQ Test Daily Test for JEE Preparation - Test: Standing Waves(17 Oct)
A resonant system has a fundamental frequency of 140 Hz. If the next frequencies that are able to give resonance are 280 Hz and 420 Hz the system could be
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A pipe has a length L and it is closed at one end for the third mode. What is the pressure graph for this pipe?
A closed organ pipe and an open organ pipe of the same length produce four beats in their fundamental mode when sounded together. If the length of the open organ pipe increases, then the number of beats will
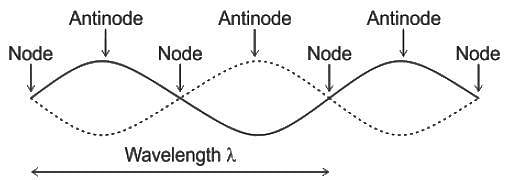
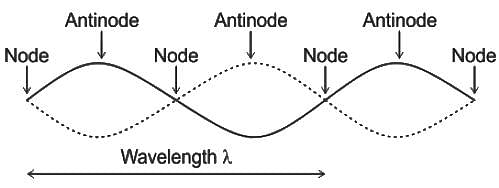
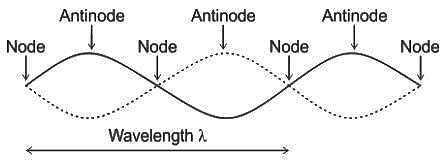
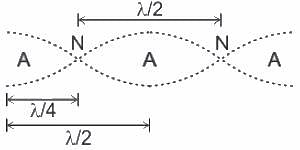
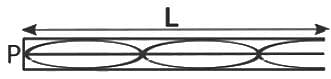
The gap between a consecutive node and anti-node in a stationary wave is?
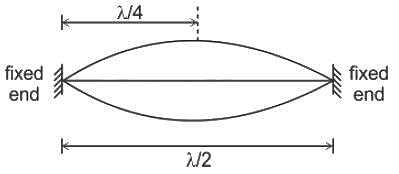
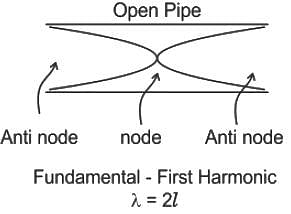
In a standing wave, in a pipe open at both ends, the first harmonic has?
For a stationary wave, if frequency is equal to ____________ then it is called fundamental mode. ('v' is the speed of travelling waves on the string of length 'L')
For a stationary wave if frequency is equal to ____________ then it is called second harmonic. (v is the speed of travelling waves on the string of length L)
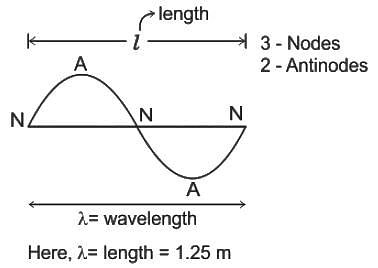
A stationary wave is produced in a string of length of 1.25 meters. If three nodes and two antinodes are produced in the string, then the wavelength of the wave is
Which of the below mentioned properties, makes difference between progressive and stationary waves
|
360 tests
|


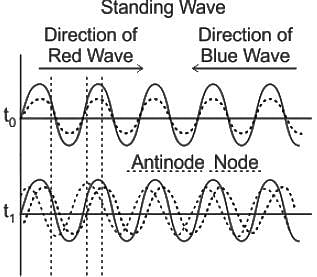

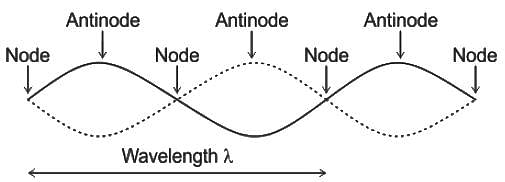
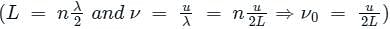
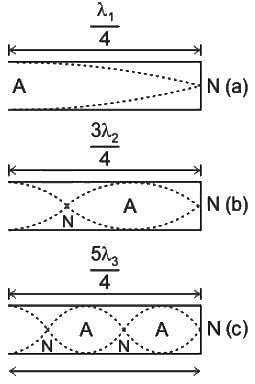
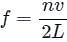 where, n is the nth harmonic, v is a velocity and L is the length of the pipe.
where, n is the nth harmonic, v is a velocity and L is the length of the pipe.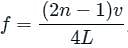 where n is a nth harmonic, v is a velocity and L is the length of the pipe.
where n is a nth harmonic, v is a velocity and L is the length of the pipe.