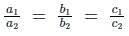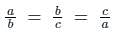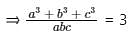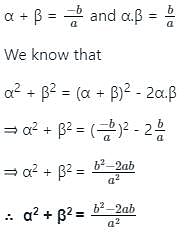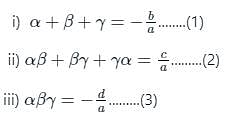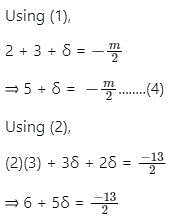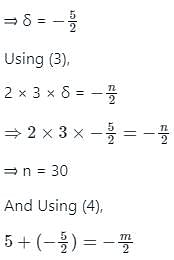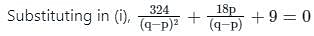Test: Quadratic Equations: Common Roots (June 9) - JEE MCQ
10 Questions MCQ Test Daily Test for JEE Preparation - Test: Quadratic Equations: Common Roots (June 9)
If (y + 2) is a common factor of ay2 + by + c and by2 + ay + c, then:
If α and β are the roots of the equation (x - a)(x - b) = c, c ≠ 0; then the roots of the equation (x - α)(x - β) +c = 0 are:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If ax2 + bx + c = 0 and bx2 + cx + a = 0 have a common root a ≠ 0 then  equal to
equal to
 equal to
equal toLet p, q(p > q) be the roots of the quadratic equation x2 + bx + c = 0 where c > 0. If p2 + q2 − 11pq = 0, then what is p − q equal to ?
If one root of the two quadratic equations x2 + ax + b = 0 and x2 + bx + a = 0 is common, then a + b is
Comprehension:
α and β are the roots of the equation ax2 + bx + b = 0.
α2 + β2 is
If 2, 3 be the roots of 2x3 + mx2 - 13x + n = 0 then the values of m and n are respectively
If the equation (m - n)x2 + (n - l)x + l - m = 0 has equal roots, then l, m and n satisfy
If x2 – hx – 21 = 0, x2 -3hx + 35 = 0(h > 0) has a common root, then the value of h is equal to
If y2 + py + 9 = 0 and y2 + qy - 9 = 0 have common roots, then p2 - q2 is equal to?
|
360 tests
|