Test: Conic Sections: Hyerbola (22 July) - JEE MCQ
15 Questions MCQ Test Daily Test for JEE Preparation - Test: Conic Sections: Hyerbola (22 July)
The eccentricity of the hyperbola 4x2–9y2–8x = 32 is
The locus of the point of intersection of the lines √3x - y - 4√3k = 0 and √3kx + ky - 4√3 = 0 for different values of k is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the latus rectum of an hyperbola be 8 and eccentricity be 3/√5 then the equation of the hyperbola is
If the centre, vertex and focus of a hyperbola be (0, 0), (4, 0) and (6, 0) respectively, then the equation of the hyperbola is
The equation of the hyperbola whose foci are (6, 5), (–4, 5) and eccentricity 5/4 is
The vertices of a hyperbola are at (0, 0) and (10, 0) and one of its foci is at (18, 0). The equation of the hyperbola is
The length of the transverse axis of a hyperbola is 7 and it passes through the point (5, –2). The equation of the hyperbola is
If the eccentricity of the hyperbola x2 – y2 sec2 a = 5 is (√3) times the eccentricity of the ellipse x2 sec2 a + y2 = 25, then a value e of a is
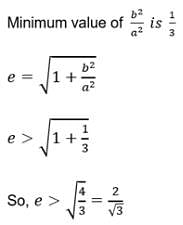
AB is a double ordinate of the hyperbola such that DAOB (where `O' is the origin) is an equilateral triangle, then the eccentricity e of the hyperbola satisfies
The locus of the point of intersection of tangents drawn at the extremities of normal chords to hyperbola xy = c2
The asymptotes of the hyperbola hx + ky = xy are
The equation of a line passing through the centre of a rectangular hyperbola is x – y –1 = 0. if one of its asymptote is 3x-4y-6 = 0, then equation of its other asymptote is
Tangents are drawn to 3x2 - 2y2 = 6 from a point P. If these tangents intersects the coordinate axes at concyclic points, The locus of P is
If the curve 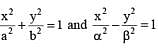 cut each other orthogonally then
cut each other orthogonally then
Let a and b be non–zero real numbers. Then, the equation (ax2 + by2 + (C) (x2 – 5xy + 6y2) = 0 represents
|
360 tests
|





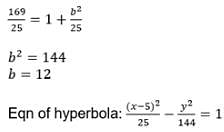

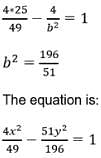

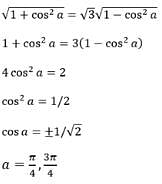

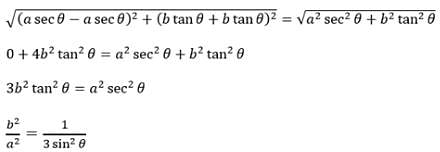
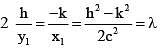
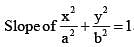
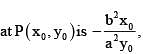
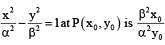
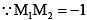
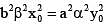 ------(1)
------(1)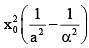
 -------(2)
-------(2)