CSIR NET Mathematics Mock Test - 10 - CSIR NET Mathematics MCQ
30 Questions MCQ Test CSIR NET Mathematics Mock Test Series - CSIR NET Mathematics Mock Test - 10
The mean of six numbers 5, 9, x – 3, x – 1, 16 and 19, is 11. The value of x is:
From the list of evaluation procedures given below identify those which will be called ‘formative evaluation’. Indicate your answer by choosing from the code:
1. A teacher awards grades to students after having transacted the course work.
2. During interaction with students in the classroom, the teacher provides corrective feedback.
3. The teacher gives marks to students on a unit test.
4. The teacher clarifies the doubts of students in the class itself.
5. The overall performance of a students is reported to parents at every three months interval.
6. The learner’s motivation is raised by the teacher through a question-answer session.
Code:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following statements defines the main objectives of Research?
If a U - 238 nucleus splits into two identical parts, the two nuclei so produced will be:
Which of the following rivers does not flow into the Arabian Sea?
A solid cannot change its shape easily compared to liquid because of :-
If 'A+B' means 'A is father of B', 'A-B' means 'A is mother of B','A*B' means 'A is brother of B' and 'A%B' means 'A is sister of B', then how is Q related to S in 'P+Q*R-S' ?
Equal masses of two liquids of densities 3 kg/m3 and 4 kg/m3 are mixed thoroughly. The density of the mixture is-
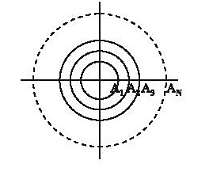
A set of concentric circles of integer radii 1, 2, ... N is shown in the figure above. An ant starts at point A1, goes round the first circle, returns to A1, moves to A2, goes round the second circle, returns to A2, moves to A3 and repeats this until it reaches AN. The distance covered by the ant is-
The partial differential equation  has the general solution:
has the general solution:
Let p(x) = αx2 + βx + γ be a polynomial where α, β, γ ∈ R. Fix X0 ∈ R.
Let 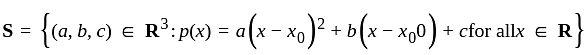
Then the number of elements in S is
A farce 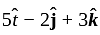 acts on a particle with position vector
acts on a particle with position vector 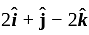 . The torque of the farce about the origin is. (December)
. The torque of the farce about the origin is. (December)
The square real matrix A is called unitary if—
The solution of the Cauchy problem for the first order PDE
 on
on 

with the initial condition x2 + y2 = 1, z = 1 is—
The general solution of the differential equation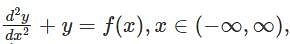 where f is a continuous, real-valued function on
where f is a continuous, real-valued function on  is (where
is (where  and k are arbitrary constants) -
and k are arbitrary constants) -
 can be transformed to
can be transformed to  for
for 
Let a, b, c be non-collinear points in the complex plane and let Δ denote the closed triangular region of the plane with vertices a, b, c. For z ∈ Δ, let h (z) = |z – a| · |z – b| · |z – c |. The maximum value of the function h—
Let A be an n × n matrix with real entries. Which of the following is correct?
Let A be a 4 × 4 invertible real matrix. Which of the following is not necessarily true?
Given a differential equation
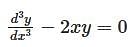
= 0 with initial conditions
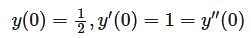
The integral equation is—
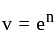 be vector space over field F = 6 then what will be one dimension of
be vector space over field F = 6 then what will be one dimension of 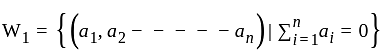
Find the correct option:
(A) The set of rational numbers is Lebesgue measurable
(B) The set of rational numbers have Lebesgue outer measure equal to zero
(C) The set of rational numbers is not Lebesgue measurable
(D) The set of rational numbers have Lebesgue out measure equal to one
Let X be a random variable with probability density function—
f(x) = α(x – μ)α – 1 e–(x – μ)α; –∞ < μ < ∞, α > 0, x > μ.
The hazard function is—
Let B be an open subset of C and ∂B denote the boundary of B. Which of the following statements are correct ?








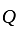
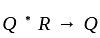 is brother of R R - S → R is mother of S
is brother of R R - S → R is mother of S
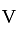
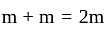
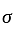
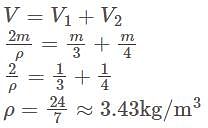
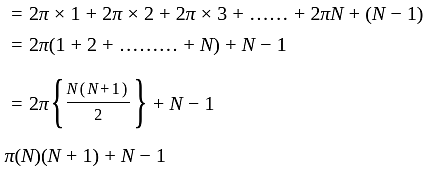



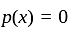 is zero polynomial
is zero polynomial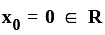
 for
for 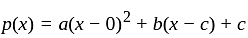
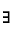 unique
unique 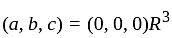
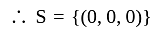
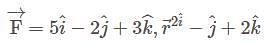
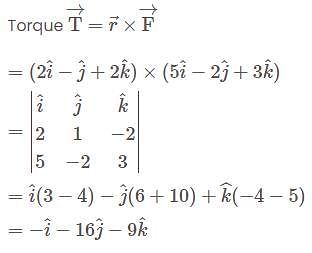
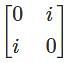 is a-
is a-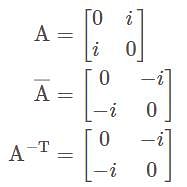
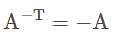


 is unbounded sequence
is unbounded sequence
 is increasing sequence
is increasing sequence  is increasing and unbounded
is increasing and unbounded is divergent
is divergent
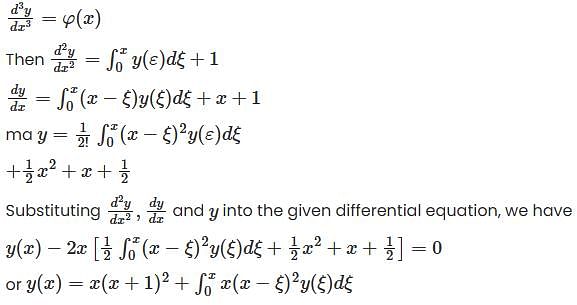
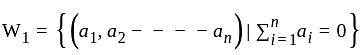
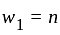
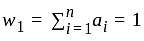
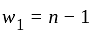
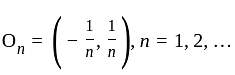
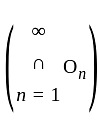 is closed set
is closed set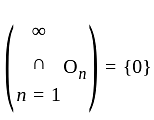
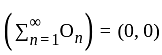
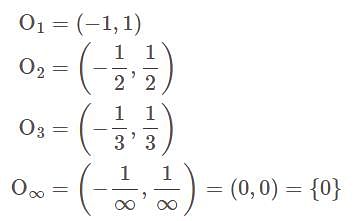
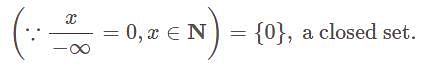
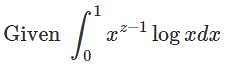
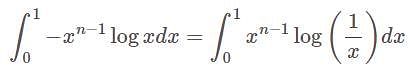
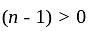 , in as much as the integrand, in that case
, in as much as the integrand, in that case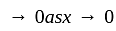 and accordingly 0, is not a point of infinite discontinuity in this case.
and accordingly 0, is not a point of infinite discontinuity in this case.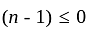 so that we have now to examine the convergence at 0. Let m be a positive number such that
so that we have now to examine the convergence at 0. Let m be a positive number such that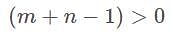
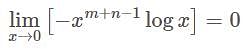
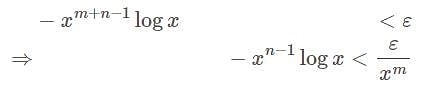
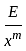 converges at 0 if and
converges at 0 if and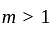 .
.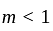 such that
such that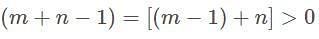
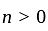 .
.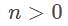
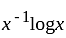 .
.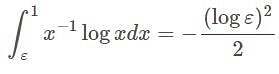
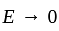 .
.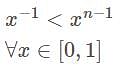

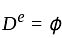 , a complement of closed set is open, therefore,
, a complement of closed set is open, therefore, 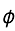 is a open set.
is a open set.














