CSIR NET Mathematics Mock Test - 3 - CSIR NET Mathematics MCQ
30 Questions MCQ Test CSIR NET Mathematics Mock Test Series - CSIR NET Mathematics Mock Test - 3
M.S. Dhoni scored 148 runs which included 8 boundaries and 3 sixes. What percent of approx.his total score did he make by running between the wickets?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following statements regarding the meaning of research are correct?
1. Research refers to a series of systematic activity or activities undertaken to find out the solution of a problem.
2. It is systematic, logical and an unbiased process wherein verification of hypothesis, data analysis, interpretation and formation of principles can be done.
3. It is an intellectual enquiry or quest towards truth.
4. It leads to enhancement of knowledge.
Select the correct answer from the codes given below:
Rs. 1200 is lent out at 5% per annum simple interest for 3 years. Find the amount after 3 years.
Find the remainder when 73 *75 *78 *57 *197 *37 is divided by 34.
In gas welding, which of the following gas is used to generate light?
The gas which causes explosions in coal mines is:
An employer reduces the number of employees in the ratio 8 : 5 and increases their wages in the ratio 7 : 9. As a result, the overall wages bill is.
If Milk is purchased at 2 Rs./litre and sold at 1/2 Rs./litre then what is the percentage profit/loss?
The general integral of the partial differential equation p2 + p3 = 1 + p1—
A firm makes two products X and Y, and has a total production capacity of 9 tonnes per day, X and Y requiring the same production capacity. The firm has a permanent contract to supply at least 2 tonnes of X and at least 3 tonnes of Y per day to another company. Each tonne of X required 20 machine hours production time and each tonne of Y requires 50 machine hours production time, the daily maximum possible number of machine-hours is 360. All the firm's output can be sold and the profit made is Rs. 80 per tonne of X and Rs. 120 per tonne of Y.
Let V be the vector space of all 2 x 2 matrices over R . Then the set W, consisting of all matrices A for which A2 = A
Let f be an one – to – one function from the closed interval [0,1] to the set of real number , -R then
The nth root of unity for k = 0,... , n - 1 are:
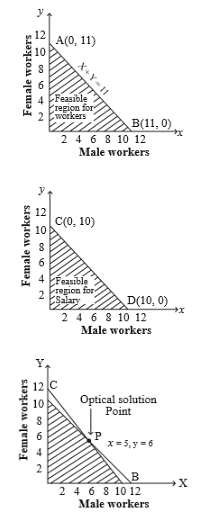
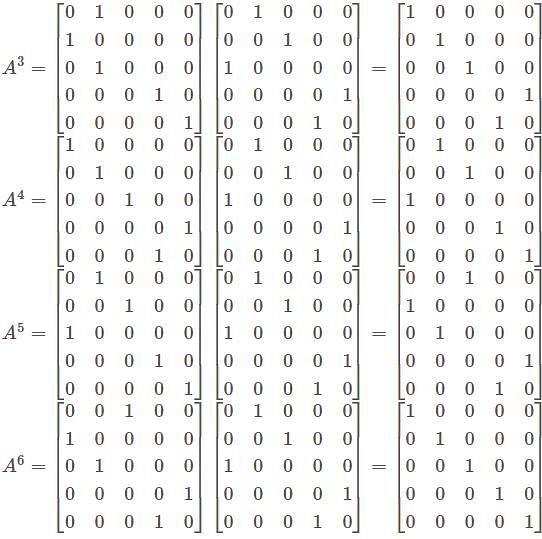
Given the permutation 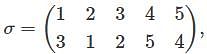 the matrix A is defined to be the one whose
the matrix A is defined to be the one whose 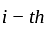 column is the
column is the 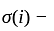 th column of the identity matrix I. which of the following is correct?
th column of the identity matrix I. which of the following is correct?
Let a, b, c be continuous functions defined on R2. Let V1, V2, V3 be nonempty subsets of R2 such that V1 ∪ V2 ∪ V3 = R2 and the PDE a(x, y)uxx + b(x, y)uxy + c(x, y)uyy = 0 iselliptic in V1, parabolic in V2 and hyperbolic in V3, then—
Consider the following row vectors :
α1 = (1, 1, 0, 1, 0, 0)
α2 = (1, 1, 0, 0, 1, 0)
α3 = (1, 1, 0, 0, 0, 1)
α4 = (1, 0, 1, 1, 0, 0)
α5 = (1, 0, 1, 0, 1, 0)
α6 = (1, 0, 1, 0, 0, 1)
The dimension of the vector space spanned by these row vectors is—
The largest interval in which the solution of IVP  exist is
exist is
If the roots of the equation x2 - 2ax + a2 + a - 3 = 0 are less than three, then a is:
select the appropiate option:
(A) The closed interval is a closed set
(B) Closed interval is open set
(C) Closed interval contains all its closure points
(D) Closed interval does not contains all its closure points
If S is a subset of Rn, if S is closed and bounded,
Suppose f : R → R is a function that satisfies | f(x) – f(y) | ≤ | x – y |β, β > 0.
Which of the following is correct ?









 [Number Multiplied]
[Number Multiplied]
 We can use any one of negative or positive remainder at any time.
We can use any one of negative or positive remainder at any time.

 Rs.2 The selling price of milk
Rs.2 The selling price of milk  Rs.
Rs. 








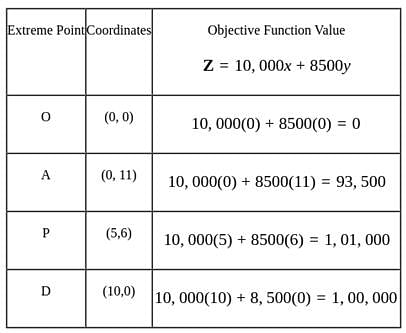
 Hence, optimal solution to the given L.P. problem is
Hence, optimal solution to the given L.P. problem is  Max.
Max. 
 and
and  has-
has-


 (2)
(2)









 at
at 
 then
then  is equal to-
is equal to-




 D is Answer
D is Answer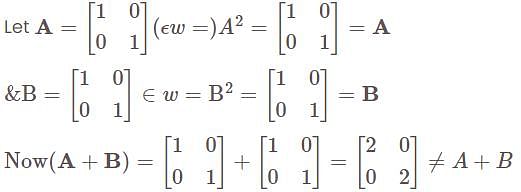
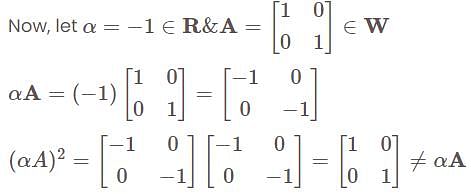
 defined by
defined by
 is one
is one  to
to  one and range of
one and range of 
 is not onto
is not onto
 Range of
Range of  contains only irrationals
contains only irrationals are not true
are not true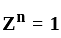
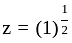
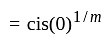
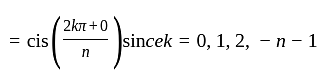
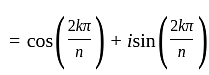
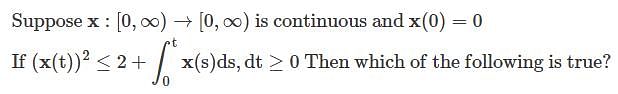
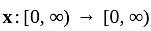 is continuous and
is continuous and 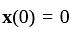
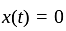
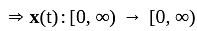 is continuous and
is continuous and 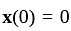

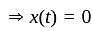 is satisfies it
is satisfies it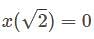
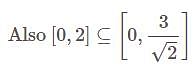
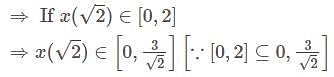
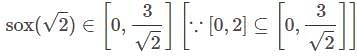
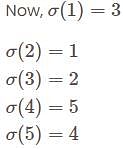

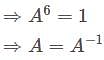
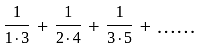 is
is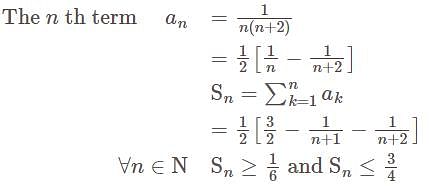
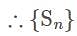 is bounded and also
is bounded and also 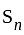 is monotone sequence
is monotone sequence
 is continuous function over the given interval
is continuous function over the given interval is bounded over the given interval
is bounded over the given interval
 where max
where max 



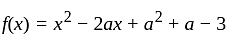
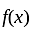 has real roots both less than 3 .
has real roots both less than 3 .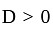 and
and 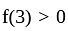
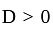
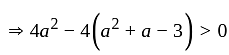
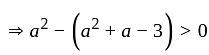
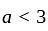 and also
and also 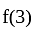 ;
;
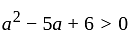
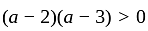
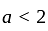 or
or 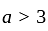
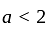 as the required condition.
as the required condition.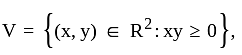 is
is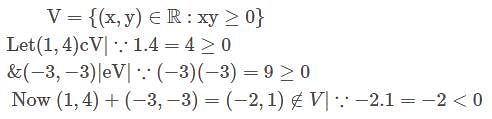
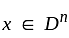 which is also an accumulation point of T and x is also accumulation point of S.
which is also an accumulation point of T and x is also accumulation point of S.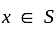 . Which proves the given statement.
. Which proves the given statement.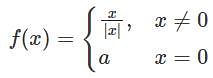
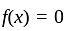 at
at 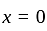
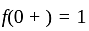
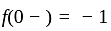
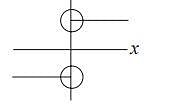
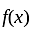 has jump at
has jump at 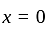
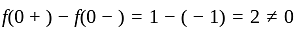
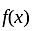 has discontinuity of first kind.
has discontinuity of first kind.














