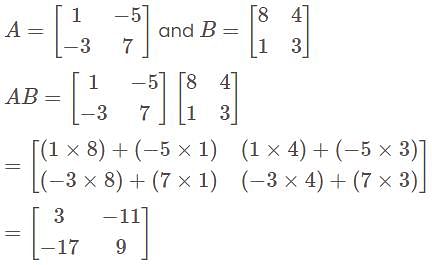CSIR NET Mathematics Mock Test - 4 - CSIR NET Mathematics MCQ
30 Questions MCQ Test CSIR NET Mathematics Mock Test Series - CSIR NET Mathematics Mock Test - 4
How many terms are there in 20, 25, 30......... 140
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Calculate the number of possible microstates when two particles are distributed in four states such that the resulting wave functions are anti-symmetric with respect to the exchange of the particle.
In which year of First World War Germany declared war on Russia and France?
If you save Rs. 1 today, Rs. 2 the next day, Rs. 3 the succeeding day and so on. What will be your total savings in 365 days?
A shopkeeper earns a profit of 12% on selling a book at 10% discount on the printed price. The ratio of the cost price and the printed price of the book is
Cost of a dianond varies directly as the square of its weight. A diamond broke into four piece with their weights in the ratio 1 : 2 : 3 : 4. If the loss in the total value of the diamond was70000, the price of the original diamond was :
Seema purchased an item for Rs.9,600 and sold it for a loss of 5 percent. From that money she purchased another item and sold it for a gain of 5 percent. What is her overall gain/ loss?
A hemispherical bowl is being filled with water at a constant volumetric rate. The level of water in the bowl increases-
Let  be a polynomial of degree
be a polynomial of degree 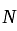 , with
, with  . Then the initial value problem
. Then the initial value problem 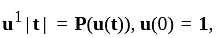 has always
has always
Let 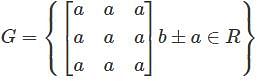 is a group w, r. t. multiplication. Then identity of the group is
is a group w, r. t. multiplication. Then identity of the group is
Let 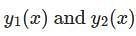 form a fundamental set of solutions of
form a fundamental set of solutions of
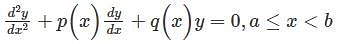
Where P(x) and q(x) are real valued continuous function on [a, b]. If 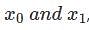 , wih
, wih 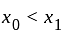 , are consecutive zeros of
, are consecutive zeros of 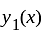 in (a, b), then
in (a, b), then
If B is the matrix obtained from A, by changing rows into columns and columns into row, then—
If the points x1, x2, …, xn are distinct, then for arbitrary real values y1, y2, …, yn the degree of the unique interpolating polynomial p(x) such that p(xi ) = yi (1 ≤ i ≤ n) is—
Amoebae are known to double in 3 min. Two identical vessels A and B, respectively contain one and two amoebae to start with. The vessel B gets filled in 3 hours. When will A get filled ?
Let f be a non constant entire function. Which of the following properties is possible for f for each z ∈ C?
Let 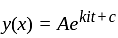 be family of curves with
be family of curves with  as 3 parameters (arbitrary) if
as 3 parameters (arbitrary) if  is the solution of
is the solution of 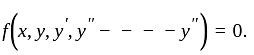 Then order of
Then order of 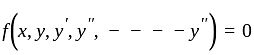 is
is
The collection C of open intervals of the form (1/n , 2/n ), n = 2 , 3,...... is an open
covering of the open interval (0, 1)
Let m be a countable additive measure defined on all sets in σ-algebra M.
If f is an extended real-valued function whose domain is measurable. The following are equivalent, for each real number, α
(A) Set {x : f(x) > α} is measurable
(B) Set {x : f(x) ≥ α} is measurable
(C) Set {x : f(x) < α} is measurable
(D) Set {x : f(x) ≤ α} is measurable
For a bivariate data set (xi, yi), i = 1, 2, …, n, suppose the least squares regression lines are—
Equation 1: 5x – 8y + 14 = 0
Equation 2: 2x – 5y + 11 = 0
Then which of the following statements are true?
Let A and B be two disjoint nonempty subsets of R2 such that A ∪ B is open in R2. Then—







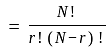
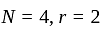







 ) is at every moment
) is at every moment  Area of cross section.
Area of cross section. is increasing ( hemisphere), the rate of change of
is increasing ( hemisphere), the rate of change of  is decreasing ( while still being positive), so
is decreasing ( while still being positive), so  is growing slower than direct proportional to time.
is growing slower than direct proportional to time.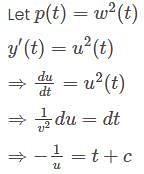

 is cube root of unity. Then
is cube root of unity. Then  is equal to
is equal to is cube root of unity
is cube root of unity and
and 






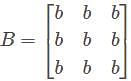 is the identity of the group G
is the identity of the group G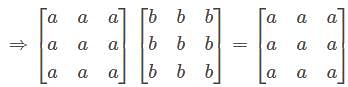
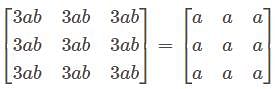
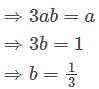
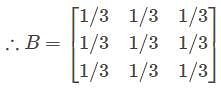
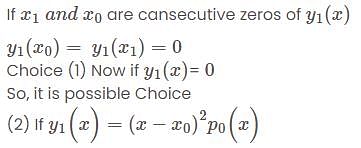
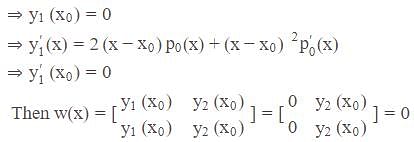
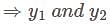 are linearly dependent Which is not true
are linearly dependent Which is not true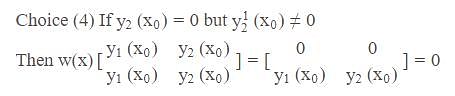
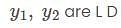
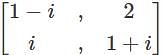 is—
is—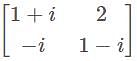
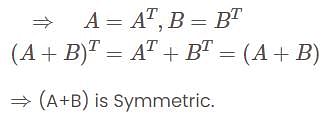
 is convergent
is convergent 
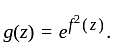 Then,
Then,  is entire (as
is entire (as  is). Now
is). Now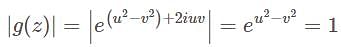
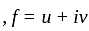 and given
and given 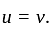 So
So 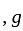 is entire and bounded and hence constant. So
is entire and bounded and hence constant. So 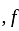 is constant ,which contradicts. So, it is FALSE.
is constant ,which contradicts. So, it is FALSE.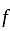 is bounded and entire and hence constant. So, it is FALSE.
is bounded and entire and hence constant. So, it is FALSE.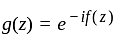 . Then
. Then 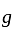 is bounded and entire and hence constant and so
is bounded and entire and hence constant and so 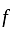 is constant. So, it is FALSE.
is constant. So, it is FALSE.




 hence we can construct a unique Green's function.
hence we can construct a unique Green's function. which satisfies the boundary condition
which satisfies the boundary condition 
 satisfies the boundary condition
satisfies the boundary condition 
 and
and  at the point
at the point 




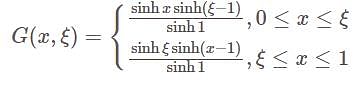
 is
is





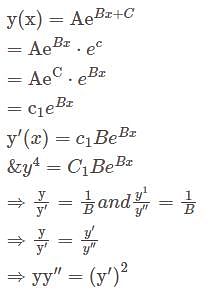
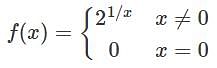
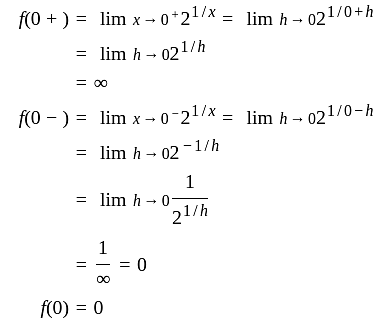
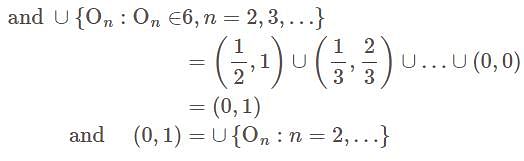
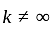
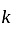
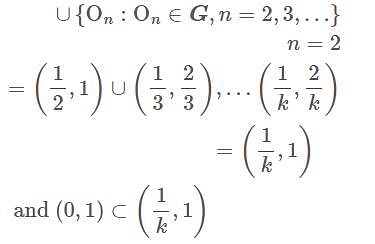
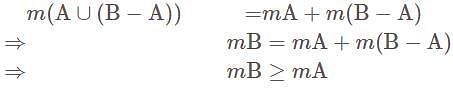
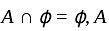 and
and 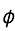 are mutually disjoint sets. By definition of countable additive measure,
are mutually disjoint sets. By definition of countable additive measure, 
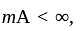 we have
we have 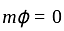
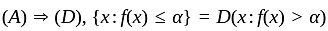
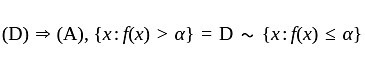
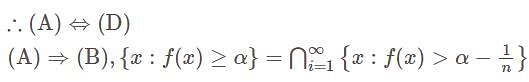
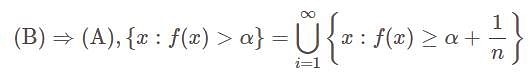
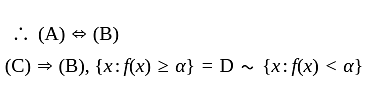
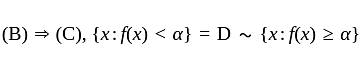
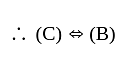
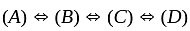
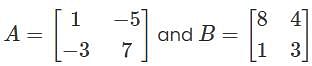 then the value of
then the value of 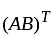 :
: