CSIR NET Mathematics Mock Test - 9 - CSIR NET Mathematics MCQ
30 Questions MCQ Test CSIR NET Mathematics Mock Test Series - CSIR NET Mathematics Mock Test - 9
In a class of 135 students, the number of boys is twice that of girls. One-sixth of the boys and one-third of the girls failed in the final examination. Find the percentage of students who passed the examination.
Made from a variety of materials, such as carbon, which inhibits the flow of current...?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In which decade was the American Institute of Electrical Engineers (AIEE) founded?
Nithya is Sam’s Sister. Mogan is Sam’s Father. Selvan is Rajan’s Son. Rajan is Mogan’s Brother. How is Nithya related to Selvan?
Lara is one year elder to Smith. Smith is two years elder to Warner. Waqar is one year elder to Warner. Who is the youngest of all?
Which one of the following is used to restore the colour of old oil paintings?
If Vishal is the brother of Anjali, Anjali is the daughter of Manoj. Manoj is brother of Rohit, and Rohit is son of Rakesh. Then how is Rohit related to Vishal?
The complete solution of z = px + qy + p2 + q2 is—
The partial differential equation  is hyperbolic in
is hyperbolic in
Let  and
and  be the solutions of the differential equation
be the solutions of the differential equation  with initial Conditions
with initial Conditions  Then
Then
Every polynomial with an odd degree has at least
A general solution of the second order equation 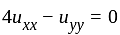 is of the form
is of the form 
Consider the quadratic equation x2 + 2Ux + V = 0 where U and V are chosen independently and randomly from {1, 2, 3} with equal probabilities. Then the probability that the equation has both roots real equals—
(X, Y) follows the bivariate normal distribution N2(0, 0, 1, 1, ρ), –1 < ρ < 1. Then,
Consider R3 with the standard inner product. Let W be the subspace of R3 spanned by (1, 0, –1). Which of the following is a basis for the orthogonal complement of W ?
Given the differential equation y"(x) –3y'(x) + 2y(x) = 5 sin x, y(0) = 1, y'(0) = – 2.
The total number of subset of a set of 6 elements is
For the set of real numbers R.
A. Sup R = + ∝
B. Inf R = – ∝
C. + ∝, – ∝ ∈ R
D. None
If c is a constant and f is measurable real valued function.
If E is a measurable set of finite measure, 〈 fn 〉 , a sequence of measurable functions defined on E.
If f is a real valued function such that for each x ∈E, fn(x)→f(x).
Consider a Markov chain on the state space {1, 2, 3, 4, 5} with transition probability matrix-
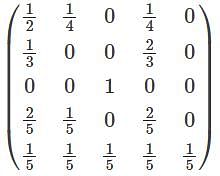
Consider the function f(z) = z2(1 – cos z), z ∈ C. Which of the following are correct ?
For any real square matrix M let λ+ (M) be the number of positive eigenvalues of M counting multiplicities. Let A be an n × n real symmetric matrix and Q be an n × n real invertible matrix. Then—






 gives
gives  ,
, 




 in the second and fourth quadrants
in the second and fourth quadrants














 are intersect then
are intersect then


 are never intersect
are never intersect
 is odd, and
is odd, and  has a root, then there must exist a real number
has a root, then there must exist a real number  with the property
with the property  .
. contains only integers and
contains only integers and  If not, we can easily multiply the values to make the assumption true. This means that
If not, we can easily multiply the values to make the assumption true. This means that  is continuous over the set of real numbers.
is continuous over the set of real numbers. as
as  goes to either infinty or minus infinity.
goes to either infinty or minus infinity. and
and  have the same sign at extreme values of
have the same sign at extreme values of  but since
but since  is odd,
is odd,  must have opposite signs for
must have opposite signs for  and
and 
 with the property
with the property  and
and 
 on the interval
on the interval  with the property
with the property  .
.
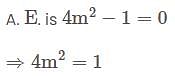
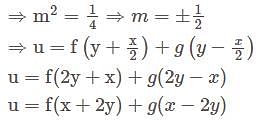
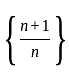 is
is
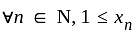 (bounded below)
(bounded below)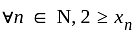 (bounded above)
(bounded above)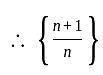 is bounded sequence
is bounded sequence
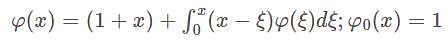
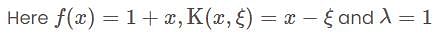
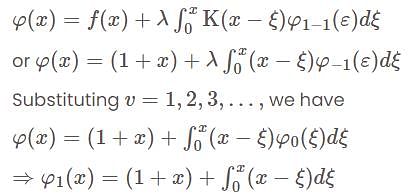
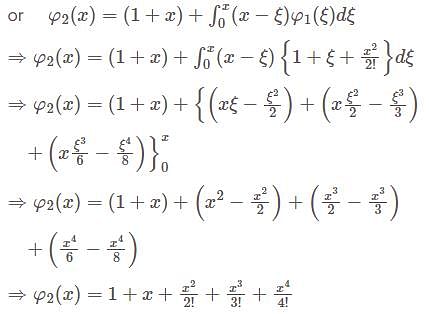
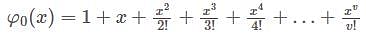
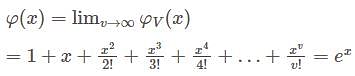
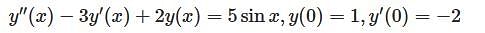
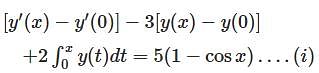
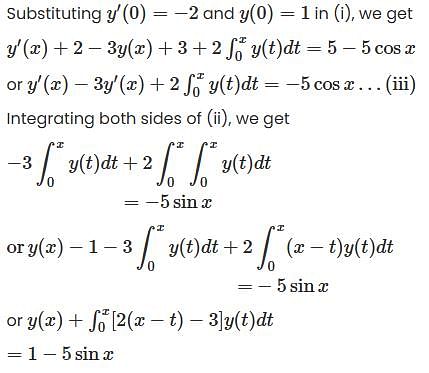
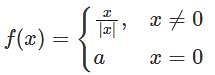
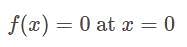
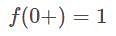
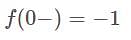
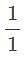
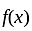 has jump at
has jump at 
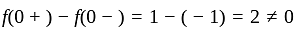
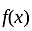 has discontinuity of first kind.
has discontinuity of first kind. let,
let,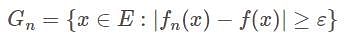
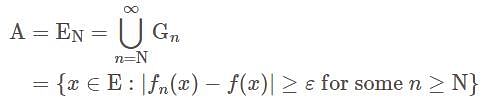
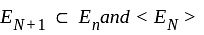 forms a decreasing sequence of measurable sets.
forms a decreasing sequence of measurable sets. and we have
and we have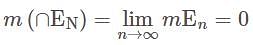
 so that
so that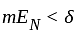 , i.e.
, i.e.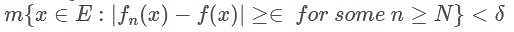
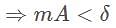

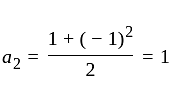
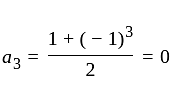
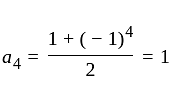
 The
The 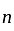 th term of the sequence
th term of the sequence















