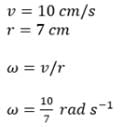Test: Measurement of Angles - Commerce MCQ
20 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Measurement of Angles
A pendulum 36 cm long oscillates through an angle of 10 degrees. Find the length of the path described by its extremity.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A wire of length 15 cm is bent to form an arc of a circle with radius 6 cm. Find in radians the angle subtended at the centre.
What is the radius of the circle in which a central angle of 60° intercepts an arc length of 48.4 cm?
A cyclist travels at the rate of 14.4 km/hr and the radius of the wheel is 35 cm. What is the measure of the angle in radian through which a spoke of the wheel will turn in one second?
What is the approximate value of 1 radian in degree measure?
A train is travelling on a curve of 350 m radius at 7 Km/hr. Through what angle will it turn in one minute?
Find the central angle of the circle whose diameter is 20 cm subtended by an arc of length 15.4 cm.
Find the length of arc of the circle whose diameter is 14 m and which subtends an angle of 1° at the centre.
What is the angle in degrees swept by the minute hand of a clock between 9.00 a.m. and 9.35 a.m.?
What will be the angle in degree if the value of the angle in radians is 5π/12
A wheel makes 360 revolutions in 1 minute. Through how many radians does it turn in 3 seconds?
What is the length of arc of a circle whose radius is 14 cm and which subtends an angle of 135° at the centre?
An object is moving on the circle of radius 7 cm in clockwise direction with a speed of 10 cm/s. find the angle in radians covered by it in 10 sec when it starts at 0 degree.
A cow is tethered to a corner of a field with a rope of length 7 m. If she grazes on the length of 210 m, what is the angle through which the rope moves?
|
75 videos|238 docs|91 tests
|
|
75 videos|238 docs|91 tests
|