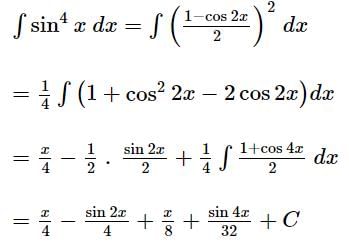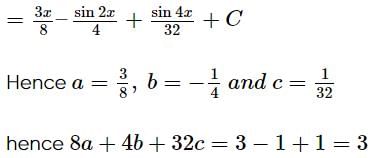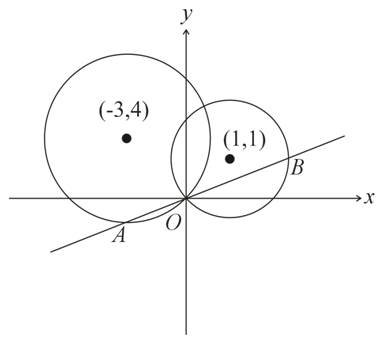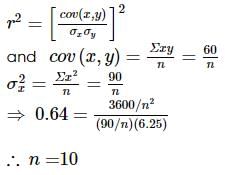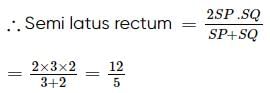AP EAMCET Mock Test - 4 - JEE MCQ
30 Questions MCQ Test - AP EAMCET Mock Test - 4
A particle moves in xy plane according to the law x = a sin ωt and y = a(1 - cos ωt), where a and w are constant. The particle traces
A semiconductor has an electron concentration of 8×1013 per cm3 and a hole concentration of 5 x 1012 per cm3. The electron mobility is 25000 cm2 V−1 s−1
and the hole mobility is 100 cm2 V. s−1 . Then,
and the hole mobility is 100 cm2 V. s−1 . Then,
A 2 μF, capacitor C1 is charged to a voltage 100 V and a 4 μF capacitor C2 is charged to a voltage 50 V. The capacitors are then connected in parallel. What is the loss of energy due to parallel connection?
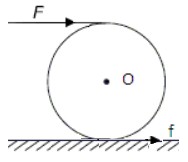
A hollow sphere of mass M and radius R is initially at rest on a horizontal rough surface. It moves under the action of a constant horizontal force F as shown in the figure.
The frictional force between the sphere and the surface is
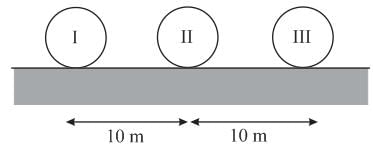
Three identical balls, ball I, ball II and ball III are placed on a smooth floor on a straight line at a separation of 10 m
between them as shown in the figure. Initially, the balls are stationary. Ball I is given a velocity of 10 m s−1 towards ball II. The collision between ball I and II is inelastic with coefficient of restitution 0.5 but collision between ball II
and III is perfectly elastic. What is the time interval between two consecutive collisions between ball I and II ?
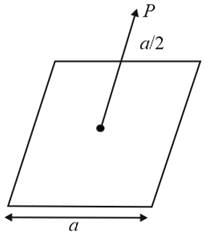
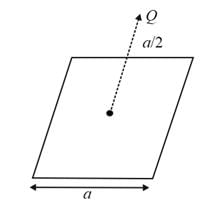
A charge Q is placed at a distance a/2 above the centre of a square surface of side length a. The electric flux through the square surface due to the charge would be?
A capillary tube of radius r is immersed in water and water rises in it to a height h. The mass of water in the capillary tube is 5 g. Another capillary tube of radius 2r is immersed in water. The mass of water, that will rise in this tube, is
If a = 18√v (where 'a' and 'v' are acceleration and velocity at any instant, respectively), then the acceleration when the time t = 1 second is
The following figure shows a spherical Gaussian surface and a charge distribution (magnitude of all the given point charges is different). When calculating the flux of electric field through the Gaussian surface, the electric field will be due to
If an unchanged capacitor is charged by connecting it to a battery, then the amount of energy lost as heat is
The number of molecules of ATP produced in the lipid metabolism of a molecule of palmitic acid is
The distance between 4x + 2y + 4z- 16 = 0 and 4x + 2y + 4z + 5 = 0 is
Which of the following diagrams correctly represents intersection of sets A and B?
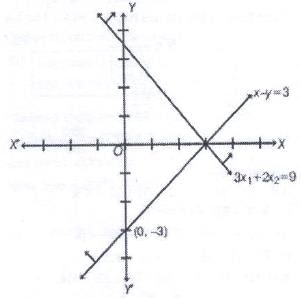
For LP.P, maximize z = 4x, + 2x2 subject to 3x1 + 2x2 ≥ 9, x1 - x2 ≤ 3, x1 ≥ 0, x2 ≥ 0 has...
The mean and variance of 7 observations are 8 and 16 respectively. If 5 observations are 2, 4, 10, 12, 14 then the remaining two observations are
The number of distinct real roots of the equation tan2 2x + 2tan2x tan3x − 1 = 0, in the interval 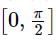 is:
is:
If 2sec2α = tanβ + cotβ, then one of the values of (α + β) {where, (α + β) is not an odd multiple of π/2} is
Let A={1, 2, 3, 4, 5, 6} and B={1, 2, 3, 4} be two sets, then the number of functions that can be defined from A to B
such that the element 2 in B has exactly 3 pre-images in A, is equal to
The line y = mx intersects the circle x2 + y2 − 2x − 2y = 0 and x2 + y2 + 6x − 8y = 0 at points A and B (points being other than origin). The range of m such that origin divides AB internally is
If x and y are deviations from arithmetic mean, r=0.8, Σxy=60 , σy=2.5 and Σx2=90, then number of items in the series is,
For any non zero vector, a,b,c
a.[(b + c) x (a + b + c)] = ...
If one of the roots of the quadratic question x2 − x = k be square of the other, then k =
If n = 1 ⋅ 2 ⋅ 3 ....m (m is a fixed positive integer > 2), then  is equal to
is equal to
The latus rectum of the parabola y2=4ax, whose focal chord is PSQ, such that SP=3 and SQ=2, is given by


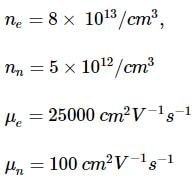
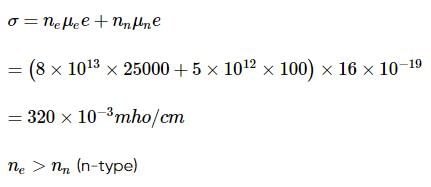

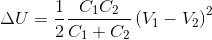
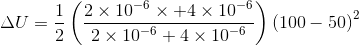
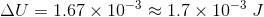
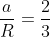 MRa
MRa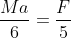 .
.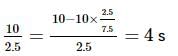
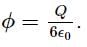
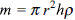
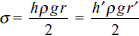
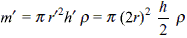
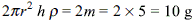
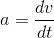
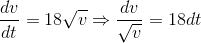
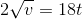
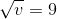
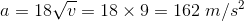
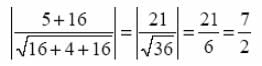
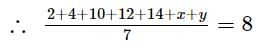
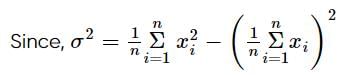
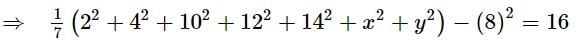
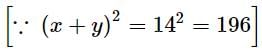
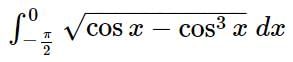
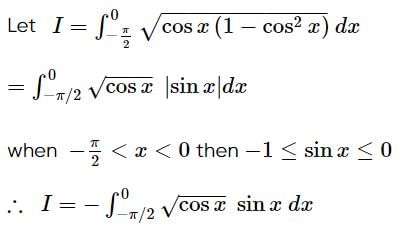
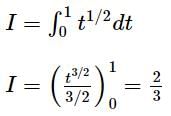
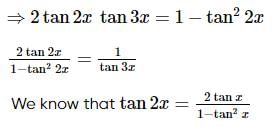
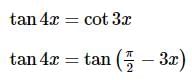

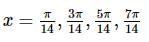
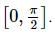
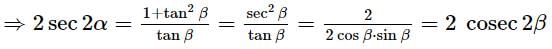
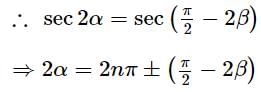
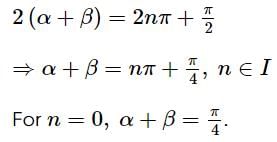
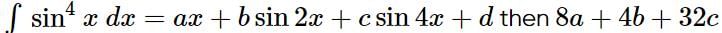 is equal to
is equal to