Mathematical Statistics - 2015 Past Year Paper - IIT JAM MCQ
30 Questions MCQ Test IIT JAM Past Year Papers and Model Test Paper (All Branches) - Mathematical Statistics - 2015 Past Year Paper
Let X1,..., Xn be a random sample from a population with probability density function
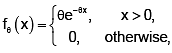
where θ > 0 is an unknown parameter.
Then, the uniformly minimum variance unbiased estimator for 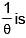
Let X1,...,X100 be independent and identically distributed N(0, 1) random variables. The correlation between 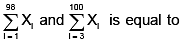
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider the problem of testing H0 : θ = 0 against H1 : θ = 1/2 based on a single observation X from U(θ, θ + 1) population. The power of the test 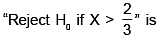
The probability mass function of a random variable X is given by
where k is a constant. The moment generating function MX(t) is
Suppose A and B are events with P(A) = 0.5, P(B) = 0.4 and = 0.2. Then P(Bc | A È B) is equal to
Let X1,..., Xn be a random sample from a Gamma(α, β) population, where β > 0 is a known constant. The rejection region of the most powerful test for H0 : α = 1 against H1 : α = 2 is of the form
Which of the following is NOT a linear transformation?
If a sequence {xn} is monotone and bounded, then
be defined by f(x) = x(x – 1)(x – 2). Then
Which of the following statements is true for all real numbers x ?
Let X1 ,..., Xn be a random sample from a Poisson (θ) population, where q > 0 is unknown. The Cramer- Rao lower bound for the variance of any unbiased estimator of g(θ) = θe-θ equals
Let X and Y be two independent random variables such that X ~ U(0, 2) and Y ~ U(1, 3).Then P(X < Y) equals
There are two boxes, each containing two components. Each component is defective with probability 1/4, independent of all other components. The probability that exactly one box contains exactly one defective component equals
Consider a normal population with unknown mean m and variance σ2 = 9. To test H0 : μ = 0 against H1 : μ ≠ 0, a random sample of size 100 is taken. Based on this sample, the test of the form rejects the null hypothesis at 5% level of significance. Then, which of the following is a possible 95%confidence interval for μ ?
Let X1 ,..., Xn be a random sample from a population with probability density function
where q > 0 is unknown. The maximum likelihood estimator of θ is
Let X1,..., Xn be a random sample from a population with probability density function
where θ > 0 is unknown. Then, a consistent estimator for θ is
Let the probability density function of a random variable X be given by
Let X be a single observation from a population having an exponential distribution with mean 1/λ. Consider the problem of testing H0 : λ = 2 against H1 : λ = 4. For the test with rejection region X > 3, let α = P(Type I error) and β = P(Type II error). Then
Let Y be an exponential random variable with mean 1/θ, where q > 0. The conditional distribution of X given Y has Poisson distribution with mean Y. Then, the variance of X is
2000 cashew nuts are mixed thoroughly in flour. The entire mixture is divided into 1000 equal parts and each part is used to make one biscuit. Assume that no cashews are broken in the process. A biscuit is picked at random. The probability that it contains no cashew nuts is
Suppose X1,...,Xn are independent random variables and Xk ~ N(0, kσ2), k = 1, ..., n, where σ2 is unknown. The maximum likelihood estimator for σ2 is
Let X1 ,..., X10 be independent and identically distributed U(–5, 5) random variables. Then, the distribution of the random variable
be a differentiable function so that f(x) f’(x) < 0 for all x. Then, which of the following is necessarily true?
Let M be the matrix Which of the following matrix equations does M satisfy?
If the determinant of an n × n matrix A is zero, then
The number of distinct real values of x for which the matrix
is singular is
is a continuous function.
Then h’(1) is equal to
Let A be a 5 × 3 real matrix of rank 2. be a non- zero vector that is in the column space of A. Let S =
Define the translation of a subspace V of
as the set x0 + V = {x0 + v : v ∈ V}. Then
a differentiable function whose derivative is continuous. Then
|
29 docs|48 tests
|
|
29 docs|48 tests
|

















