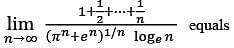Mathematical Statistics - 2019 Past Year Paper - IIT JAM MCQ
30 Questions MCQ Test IIT JAM Past Year Papers and Model Test Paper (All Branches) - Mathematical Statistics - 2019 Past Year Paper
Let {xn }n > 1 be a sequence of positive real numbers. Which one of the following statements is always TRUE?
Consider the function f (x, y) = x3 − 3xy2, x,y ∈ ℝ. Which one of the following statements is TRUE?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If F(x) = 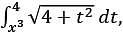 for x ∈ ℝ, then F′(1) equals
for x ∈ ℝ, then F′(1) equals
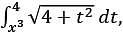 for x ∈ ℝ, then F′(1) equals
for x ∈ ℝ, then F′(1) equalsLet T: ℝ2 → ℝ2 be a linear transformation such that  Suppose that
Suppose that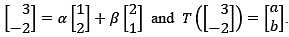 Then α + β + a + b equals
Then α + β + a + b equals
Two biased coins C1 and C2 have probabilities of getting heads 2/3 and 3/4 , respectively, when tossed. If both coins are tossed independently two times each, then the probability of getting exactly two heads out of these four tosses is
Let X be a discrete random variable with the probability mass function
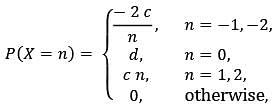
where c and d are positive real numbers. If P(|X| ≤ 1) = 3/4, then E(X) equals
Let X be a Poisson random variable and P(X = 1) + 2 P(X = 0) = 12 P(X = 2). Which one of the following statements is TRUE?
Let X1, X2, … be a sequence of i.i.d. discrete random variables with the probability mass function
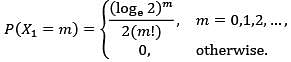
If Sn = X1 + X2 + ⋯ + Xn , then which one of the following sequences of random variables converges to 0 in probability?
Let X1, X2, … , Xn be a random sample from a continuous distribution with the probability density function
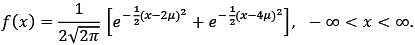
If T = X1 + X2 + ⋯ + Xn , then which one of the following is an unbiased estimator of μ?
Let X1, X2, … , Xn be a random sample from a N(θ, 1) distribution. Instead of observing X1, X2, … , Xn, we observe Y1, Y2, … , Yn , where Yi = eXi , i = 1, 2, … , n. To test the hypothesis
H0: θ = 1 against H1: θ ≠ 1
based on the random sample Y1, Y2, … , Yn , the rejection region of the likelihood ratio test is of the form, for some c1 < c2 ,
A possible value of b ∈ ℝ for which the equation x4 + bx3 + 1 = 0 has no real root is
Let the Taylor polynomial of degree 20 for 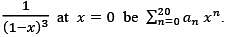 Then a15 is
Then a15 is
The length of the curve  from x = 1 to x = 8 equals
from x = 1 to x = 8 equals
The volume of the solid generated by revolving the region bounded by the parabola x = 2y2 + 4 and the line x = 6 about the line x = 6 is
Let P be a 3 × 3 non-null real matrix. If there exist a 3 × 2 real matrix Q and a 2 × 3 real matrix R such that P = QR, then
If P = and 6P−1 = aI3 + bP − P2, then the ordered pair (a, b) is
and 6P−1 = aI3 + bP − P2, then the ordered pair (a, b) is
Let E, F and G be any three events with P(E) = 0.3, P(F|E) = 0.2, P(G|E) = 0.1 and P (F ∩ G|E) = 0.05. Then P(E − (F ∪ G)) equals
Let E and F be any two independent events with 0 < P(E) < 1 and 0 < P(F) < 1. Which one of the following statements is NOT TRUE?
Let X be a continuous random variable with the probability density function
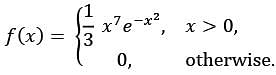
Then the distribution of the random variable W = 2x2 is
Let X be a continuous random variable with the probability density function
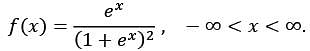
Then E (X) and P(X > 1), respectively, are
The lifetime (in years) of bulbs is distributed as an Exp(1) random variable. Using Poisson approximation to the binomial distribution, the probability (round off to 2 decimal places) that out of the fifty randomly chosen bulbs at most one fails within one month equals
Let X follow a beta distribution with parameters m (> 0) and 2. If P 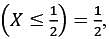 then Var(X) equals
then Var(X) equals
Let X1, X2 and X3 be i.i.d. U(0,1) random variables. Then P(X1 > X2 + X3) equals
Let X and Y be i.i.d. U(0, 1) random variables. Then E(X| > Y) equals
Let −1 and 1 be the observed values of a random sample of size two from N(θ, θ) distribution. The maximum likelihood estimate of θ is
Let X1 and X2 be a random sample from a continuous distribution with the probability density function
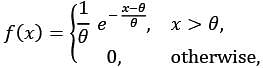
where θ > 0. If X(1) = min{X1, X2} and 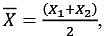 then which one of the following statements is TRUE?
then which one of the following statements is TRUE?
Let X1, X2, … , Xn be a random sample from a continuous distribution with the probability density function f(x). To test the hypothesis

the rejection region of the most powerful size α test is of the form, for some c > 0,
Let X1, X2, … , Xn be a random sample from a N(θ, 1) distribution. To test H0: θ = 0 against H1: θ = 1, assume that the critical region is given by 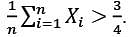 Then the minimum sample size required so that P(Type I error) ≤ 0.05 is
Then the minimum sample size required so that P(Type I error) ≤ 0.05 is
|
29 docs|48 tests
|
|
29 docs|48 tests
|