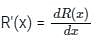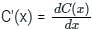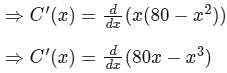Test: Minima & Maxima - 1 - Civil Engineering (CE) MCQ
15 Questions MCQ Test Engineering Mathematics - Test: Minima & Maxima - 1
If 3 ≤ x ≤ 10 and 5 ≤ y ≤ 15, then maximum value of (x / y) is-
A manufacturing company has its variable cost given by C(x) = x(80 - x2) where 'x' is the number of quantities produced. The price per unit is p(x) = 5x where 'x' is the number of units in demand. The ratio of marginal cost and marginal revenue when 5 units were both produced and in demand -
If f(x) = |x + 1| + |x + 10|, then find the minimum value of f(x).
If the minimum value of expression x2 + 5x + p = 0 is (-1/4), then find the value of p.
A rectangle is given with a perimeter of 48 cm. If the rectangle encloses maximum area possible, then the area of the rectangle will be
Find the difference between the maximum value of -3x2 + 2x + 13 = 0 and the minimum value of x2 - 2x + 3 = 0.
If x is real, then find the minimum value of (3x2 - 2x + 8).
If N is a four digit number formed by digits x1, x2, x3 and x4, then maximum value of 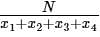 is-
is-
A manufacturing firm has its variable cost given by C(x) = x(12 - x3) where 'x' is the number of quantities produced. The price per unit is p(x) = 6x - 2 where 'x' is the number of units in demand. The ratio of marginal cost and marginal revenue when 3 units were both produced and in demand -
|
65 videos|120 docs|94 tests
|


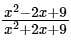 are
are