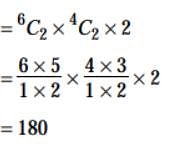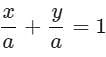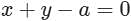NDA Mock Test: Mathematics - 3 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Mock Test Series 2024 - NDA Mock Test: Mathematics - 3
If f(x) = ax + b and g(x) = cx + d, then f[g(x)] – g[f(x)] is equivalent to
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The set O of odd positive integers less than 10 can be expressed by ______
The amplitude of a complex number is called the principal value amplitude if it lies between.
A lady arranges a dinner party for 6 guests .The number of ways in which they may be selected from among 10 friends if 2 of the friends will not attend the party together is
In how many ways can a mixed doubles tennis game be arranged from a group of 10 players consisting of 6 men and 4 women
In how many ways can a cricket team of 11 players be chosen out from a squad of 14 players, if 5 particular players are always chosen?
A team of 7 players is to be formed out of 5 under 19 players and 6 senior players. In how many ways, the team can be chosen when at least 4 senior players are included?
In the expansion of (x+y)n, the coefficients of 4th and 13th terms are equal, Then the value of n is :
What is the general term in the expansion of (2y-4x)44?
The coefficient of x4 in the expansion of (1 + x + x2 + x3)n is:
If in the expansion of (1 + x)m (1 – x)n, the co-efficients of x and x2 are 3 and – 6 respectively, then m is [JEE 99,2 ]
Find the largest co-efficient in the expansion of (1 + x)n, given that the sum of co-efficients of the terms in its expansion is 4096. [REE 2000 (Mains)]
The first 4 terms of the sequence a1 = 2, an = 2an-1 + 1 for n > 2 are
The value of y, for the line passing through (3, y) and (2, 7) is parallel to the line passing through (-1 , 4) and (0, 6) is:
Slope of a line which cuts intercepts of equal lengths on the axes is:
The line through the point (a, b) and parallel to the line Ax + By + C = 0 is:
Find the perpendicular distance from the origin of the line x + y – 2 = 0 is:
The equation of a line whose perpendicular distance from the origin is 8 units and the angle made by perpendicular with positive x-axis is 60 degree is:
A line is equally inclined to the axis and the length of perpendicular from the origin upon the line is √2. A possible equation of the line is
The lines y = mx , y + 2x = 0 , y = 2x + λ and y = - mx + λ form a rhombus if m =
The locus of a variable point whose distance from the point (2, 0) is 2/3 times its distance from the line x = 9/2 is
|
2 docs|101 tests
|
|
2 docs|101 tests
|