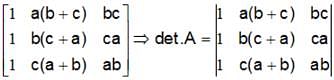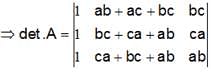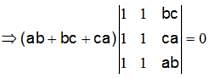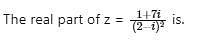NDA Mock Test: Mathematics - 1 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Mock Test Series 2024 - NDA Mock Test: Mathematics - 1
Let X = {x | x = 2 + 4k, where k = 0, 1, 2, 3,...24}. Let S be a subset of X such that the sum of no two elements of S is 100. What is the maximum possible number of elements in S ?
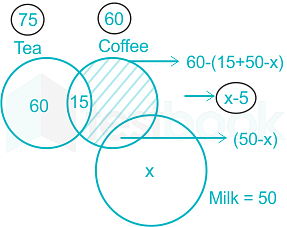
In a party of 150 persons, 75 persons take tea, 60 persons take coffee and 50 persons take milk. 15 of them take both tea and coffee, but no one taking milk takes tea. If each person in the party takes at least one drink, then what is the number of persons taking milk only ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If R is a relation from a non – empty set A to a non – empty set B, then
Let R be the relation over the set of straight lines of a plane such that l1 R l2 ⇔ l1 ⊥ l2. Then, R is
Let f be a function such that f(mn) = f(m) f(n) for every positive integers m and n. If f(1), f(2) and f(3) are positive integers, f(1) < f(2), and f(24) = 54, then f(18) equals
(2019)
Let f(x) = min{2x2, 52 − 5x}, where x is any positive real number. Then the maximum possible value of f(x) is
(2018)
Let a, b, c, d, u, v be integers. If the system of equations, a x + b y = u, c x + dy = v, has a unique solution in integers, then
The complex numbers z = x + iy which satisfy the equation 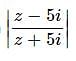 = 1 lie on
= 1 lie on
The inequality | z − 4 | < | z −2 | represents the region given by
A lady wants to select one cotton saree and one polyster saree from a textile shop. If there are 15 cotton and 13 polyster varieties in that shop, in how many ways can she pick up two sarees?
In a class, there are 30 boys and 18 girls. The teacher wants to select one boy and one girl to represent the class for quiz competition. In how many ways can the teacher make this selection?
In the expansion of (a+b)n, N the number of terms is:
Find the value of r, if the coefficients of (2r + 4)th and (r – 2)th terms in the expansion of (1 + x)18 are equal.
If we want to insert 8 numbers between the numbers 4 and 31 such that the resulting sequence is an AP.The difference between the consecutive numbers will be
For what value of n, is the arithmetic mean (AM) of a and b?
is the arithmetic mean (AM) of a and b?
The digits of a positive integer having three digits are in AP and sum of their digits is 21. The number obtained by reversing the digits is 396 less than the original number. Find the original number.
Find the value of x for which the points (1,3) , (-2, 9) and (x, -1) are collinear.
The ratio in which the point R (1, 2) divides the line segment joining points P (2, 3) and Q (3, 5) is:
What will be the new equation of the straight line 3x + 4y = 15, if the origin gets shifted to (1,-3) ?
What will be the new equation of the straight line 5x + 8y = 10, if the origin gets shifted to (2,-3) ?
|
1 docs|91 tests
|
|
1 docs|91 tests
|



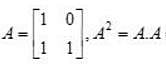
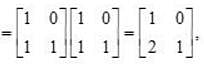
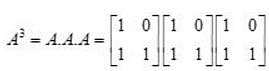
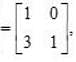
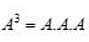
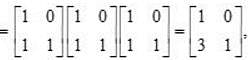
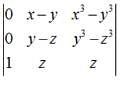
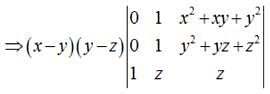
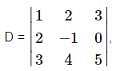 , then
, then 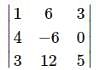 is equal to
is equal to 
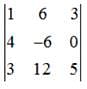
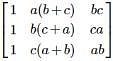 , then Det. A is
, then Det. A is