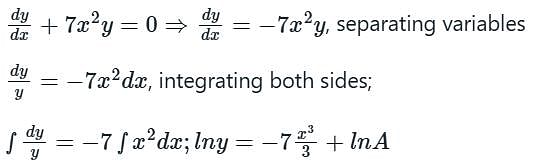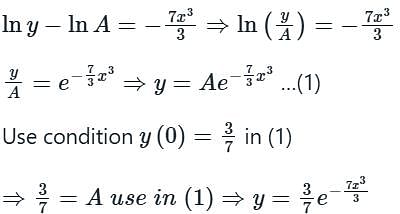Test: First Order Nonlinear PDE - Civil Engineering (CE) MCQ
10 Questions MCQ Test Engineering Mathematics - Test: First Order Nonlinear PDE
Which of the following represents Lagrange’s linear equation?
Which of the following equations represents Clairaut’s partial differential equation?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following is a type of Iterative method of solving non-linear equations?
Which of the following is not a standard method for finding the solutions for differential equations?
Which of the following is an example of non-linear differential equation?
Solution of a differential equation is any function which satisfies the equation.
A solution which does not contain any arbitrary constants is called a general solution.
Singular solution of a differential equation is one that cannot be obtained from the general solution gotten by the usual method of solving the differential equation.
A particular solution for an equation is derived by substituting particular values to the arbitrary constants in the complete solution.
For the equation ay/dx 7x2y = 0, if y(0) = 3/7, then the value of y(1) is
|
65 videos|120 docs|94 tests
|
|
65 videos|120 docs|94 tests
|